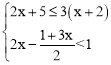题目内容
【题目】如图，已知抛物线顶点D（-1，-4），且过点C（0，-3）.
（1）求此二次函数的解析式；
（2）抛物线与x轴交于点A、B，在抛物线上存在一点P使△ABP的面积为10，请直接写出点P的坐标．
【答案】（1）y=x+2x-3；（2）点P的坐标（-4,5）或（2,5）
【解析】试题分析：（1）利用待定系数法把D（-1，-4），C（0，-3）代入二次函数y=a(x-h)2+k中，即可算出a的值，进而得到函数解析式是y=x2+2x-3；
（2）首先求出A、B两点坐标，再算出AB的长，再设P（m，n），根据△ABP的面积为10可以计算出n的值，然后再利用二次函数解析式计算出m的值即可得到P点坐标．
试题解析：（1）设函数的解析式为y=a(x-h)2+k，
∵顶点D（-1，-4），且过点C（0，-3），
∴-3=a(0+1)2-4解得a=1，
所以函数的解析式y=(x+1)2-4，
即：y=x+2x-3 .
（2）∵当y=0时，x2+2x-3=0，
解得：x1=-3，x2=1；
∴A（1，0），B（-3，0），
∴AB=4，
设P（m，n），
∵△ABP的面积为10，
∴
AB|n|=10，
解得：n=±5，
当n=5时，m2+2m-3=5，
解得：m=-4或2，
∴P（-4，5）（2，5）；
当n=-5时，m2+2m-3=-5，
方程无解，
故P（-4，5）（2，5）.
【题目】随着“互联网+”时代的到来，一种新型打车方式受到大众欢迎，该打车方式的总费用由里程费和耗时费组成，其中里程费按x元/公里计算，耗时费按y元/分钟计算（总费用不足9元按9元计价）．小明、小刚两人用该打车方式出行，按上述计价规则，其打车总费用、行驶里程数与打车时间如表：
时间（分钟） | 里程数（公里） | 车费（元） | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
（1）求x，y的值；
（2）如果小华也用该打车方式，打车行驶了11公里，用了14分钟，那么小华的打车总费用为多少？
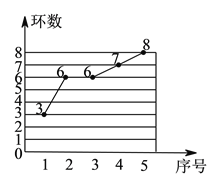
【题目】教练想从甲、乙两名运动员中选拔一人参加射击锦标赛，故先在射击队举行了一场选拔比赛．在相同的条件下各射靶
次，每次射靶的成绩情况如图所示．
甲射靶成绩的条形统计图
| 乙射靶成绩的折线统计图
|
（
）请你根据图中的数据填写下表：
平均数 | 众数 | 方差 | |
甲 | __________ |
|
|
乙 |
| __________ | __________ |
（
）根据选拔赛结果，教练选择了甲运动员参加射击锦标赛，请给出解释．
