题目内容
【题目】如图,正方形ABCD内的△BEC为正三角形,求∠DEA的度数.
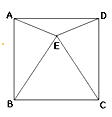
【答案】150°.
【解析】
由四边形ABCD是正方形和△BEC是正三角形,得出△BAE是等腰三角形,∠ABE=30°,由等腰三角形的性质得出∠BAE=75°,求出∠EAD=15°,同理∠EDA=15°,最后由三角形内角和求出∠DEA的度数.
解:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=∠DAB=90°.
∵△BEC是正三角形,
∴BE=BC=EC,∠EBC=∠BEC=∠ECB=60°.
∴BA=BE(即△BAE是等腰三角形),
∠ABE=∠ABC-∠EBC= 90°-60°=30°,
∴∠BAE=∠BEA=![]() =75°,
=75°,
∴∠EAD=∠BAD-∠BAE=90°-75°=15°.
同理∠EDA=15°,
∴∠DEA=180°-∠EAD-∠EDA=180°-15°-15°=150°.

练习册系列答案
相关题目