Question

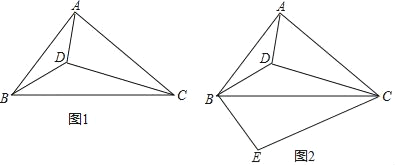
【题目】如图1，设D为锐角△ABC内一点，∠ADB=∠ACB+90°．

（1）求证：∠CAD+∠CBD=90°；

（2）如图2，过点B作BE⊥BD，BE=BD，连接EC，若ACBD=ADBC，

①求证：△ACD∽△BCE；

②求的值．

Answer 1

【答案】（1）详见解析；（2）①详见解析；②=.

【解析】

（1）如图1，延长CD交AB于E，根据三角形外角的性质得到∠ADE=∠CAD+∠ACD，∠BDE=∠CBD+∠BCD，结合已知条件∠ADB=∠ACB+90°．即可证明.

（2）①∠CAD+∠CBD=90°，∠CBD+∠CBE=90°，根据同角的余角相等即可得到∠CAD=∠CBE，根据ACBD=ADBC，BD=BE，即可得到根据相似三角形的判定方法即可判定△ACD∽△BCE；

②连接DE，根据BE⊥BD，BE=BD，得到△BDE是等腰直角三角形，根据等腰直角三角形的性质得到分别判定△ACD∽△BCE，△ACB∽△DCE，根据相似三角形的性质得到则

证明：（1）如图1，延长CD交AB于E，

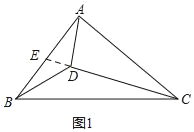
∵∠ADE=∠CAD+∠ACD，

∠BDE=∠CBD+∠BCD，

∴∠ADB=∠ADE+∠BDE=∠CAD+∠CBD+∠ACB，

∵∠ADB=∠ACB+90°．

∴∠CAD+∠CBD=90°；

（2）①如图2，∵∠CAD+∠CBD=90°，∠CBD+∠CBE=90°，

∴∠CAD=∠CBE，

∵ACBD=ADBC，BD=BE，

∴

∴△ACD∽△BCE；

②如图2，连接DE，

∵BE⊥BD，BE=BD，

∴△BDE是等腰直角三角形，

∴

∵△ACD∽△BCE，

∴∠ACD=∠BCE，

∴∠ACB=∠DCE，

∵

∴△ACB∽△DCE，

∴

∴