题目内容
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两知直线,给出它们平行的定义:设一次函数y=k1x+b(k1≠0)的图象为直线l1,一次函数y=k2x+b(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.如图,将直线y=4x沿y轴向下平移后,得到的直线与x轴交于点A(
| 9 |
| 4 |
 双曲线y=
双曲线y=| k |
| x |
(1)求直线AB的解析式;
(2)若点B的纵坐标为m,求双曲线解析式(用含m的代数式表示).
分析:(1)根据题意,设直线AB的解析式为y=4x+b.将点A(
,0)的坐标代入可得b的值,即可得答案;
(2)设点B的坐标为(xB,m),由直线AB经过点B,可得B的坐标与x的关系,又由点B在双曲线y=
(x>0)上,进而可得双曲线解析式.
| 9 |
| 4 |
(2)设点B的坐标为(xB,m),由直线AB经过点B,可得B的坐标与x的关系,又由点B在双曲线y=
| k |
| x |
解答:解:(1)将直线y=4x沿y轴向下平移后经过x轴上点A(
,0),
设直线AB的解析式为y=4x+b.(1分)
则4×
+b=0.
解得b=-9.(3分)
∴直线AB的解析式为y=4x-9.(4分)
(2)设点B的坐标为(xB,m),
∵直线AB经过点B,(5分)
∴m=4xB-9.∴xB=
.(6分)
∴B点的坐标为(
,m),(7分)
∵点B在双曲线y=
(x>0)上,
∴m=
.
∴k=
.(9分)
∴双曲线解析式为:y=
=
.(10分)

| 9 |
| 4 |
设直线AB的解析式为y=4x+b.(1分)
则4×
| 9 |
| 4 |
解得b=-9.(3分)
∴直线AB的解析式为y=4x-9.(4分)
(2)设点B的坐标为(xB,m),
∵直线AB经过点B,(5分)
∴m=4xB-9.∴xB=
| m+9 |
| 4 |
∴B点的坐标为(
| m+9 |
| 4 |
∵点B在双曲线y=
| k |
| x |
∴m=
| k | ||
|
∴k=
| m2+9m |
| 4 |
∴双曲线解析式为:y=
| ||
| x |
| m2+9m |
| 4x |

点评:本题考查了二次函数、一次函数解析式的确定,同学们要注意根据实际情况,选用合适的方法解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 我们就称直线l1与直线l2互相平行.解答下面的问题:
我们就称直线l1与直线l2互相平行.解答下面的问题: 阅读下面的材料:
阅读下面的材料: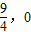 ),与双曲线
),与双曲线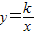 (x>0)交于点B.
(x>0)交于点B.

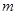 :y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
:y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.