题目内容
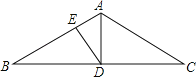
【题目】如图,在△ABC中,AB=AC,∠BAC=120°,D是BC的中点,DE⊥AB于点E,若EA=2,则BE=( )
A.3 B.4 C.6 D.8
【答案】C
【解析】
试题分析:根据在△ABC中,AB=AC,∠BAC=120°,D是BC的中点,DE⊥AB于点E,EA=2,可以求得AD⊥BC,∠B=∠C,以及∠B和∠C的度数,从而可以求得AD、AB的长,从而可以求得BE的长,本题得以解决.
解:∵在△ABC中,AB=AC,∠BAC=120°,D是BC的中点,
∴AD⊥BC,∠B=∠C=30°,
∴∠ADC=90°,
∵DE⊥AB于点E,EA=2,
∴∠DEA=90°,∠DEB=90°,
∴∠BAD=60°,∠EDA=30°,
∴AD=2AE=4,
∴AB=2AD=8,
∴BE=AB﹣AE=8﹣2=6,
故选C.

练习册系列答案
相关题目