题目内容
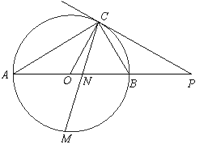
【题目】如图,在△ABC中,AB=AC=8,BC=6,点D为BC上一点,BD=2.过点D作射线DE交AC于点E,使∠ADE=∠B.求线段

【答案】1
解:∵AB=AC,∴∠B=∠C.∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠CDE,而∠ADE=∠B,∴∠BAD=∠CDE,∴△ABD∽△DCE,
∴![]() =
=![]() .∵AB=8,BC=6,BD=2,∴DC=BC-BD=4,∴
.∵AB=8,BC=6,BD=2,∴DC=BC-BD=4,∴![]() =
=![]() ,∴CE=1.
,∴CE=1.
【解析】试题分析:由条件可得到![]() 可证明
可证明![]() 由相似三角形的性质可得到
由相似三角形的性质可得到![]() 代入可求得
代入可求得![]() .
.
试题解析:∵AB=AC,
∴∠B=∠C.
∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠CDE,
而∠ADE=∠B,
∠BAD=∠CDE,
∴△ABD∽△DCE,
![]()
∵AB=8,BC=6,BD=2,
∴DC=BC-BD=4,
![]()
∴CE=1.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目