题目内容
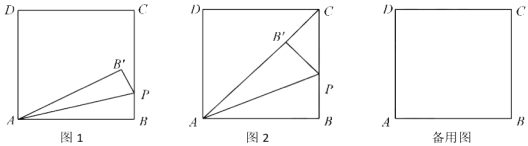
【题目】如图1,在矩形![]() 中,BC=3,动点
中,BC=3,动点![]() 从
从![]() 出发,以每秒1个单位的速度,沿射线
出发,以每秒1个单位的速度,沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]()
(1)若![]()
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
(2)当P点不与C点重合时,若直线PB’与直线CD相交于点M,且当t<3时存在某一时刻有结论∠PAM=45°成立,试探究:对于t>3的任意时刻,结论∠PAM=45°是否总是成立?请说明理由.
【答案】(1)①![]() ;②t=2或t=6或t=2
;②t=2或t=6或t=2![]() (2)见解析.
(2)见解析.
【解析】
(1)①先利用勾股定理求出AC长,再根据△APB≌△APB′,继而根据全等三角形的性质推导得出∠B=∠PB′C=90°,B′C= ![]() ,再证明
,再证明![]() ,根据相似三角形的性质求出PB′=2
,根据相似三角形的性质求出PB′=2![]() -4,由此即可求得答案;
-4,由此即可求得答案;
②根据题意分三种情况,分别画出图形,结合图形分别讨论求解即可;
(2)如图,根据∠PAM=45°以及翻折的性质可以证明得到△DAM≌△B′AM,从而可得AD=AB′=AB,证得四边形ABCD是正方形,继而根据题意画出图形,根据翻折的性质以及全等三角形的知识进行推导即可求得答案.
(1)①∵四边形ABCD是矩形,
∴∠B=90°,
∴AC=![]() ,
,
∵△APB≌△APB′,
∴∠AB′P=∠B=90°,AB′=AB=2![]() ,BP=B′P,
,BP=B′P,
∴∠B=∠PB′C=90°,B′C=AC-AB′=![]() ,
,
又∵∠PCB′=∠ACB,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴PB′=2![]() -4,
-4,
∴PB=2![]() -4,
-4,
即t=2![]() -4;
-4;
②如图,当∠PCB′=90 °时,此时点B′落在BC上,
在Rt△AB′D中,∠D=90°,∴B′D=![]() ,
,
∴B′C=![]() ,
,
在△PCB′中,由勾股定理得:![]() ,
,
解得t=2;
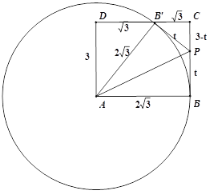
如图,当∠PCB′=90 °时,此时点B′在CD的延长线上,
在Rt△AB′D中,∠ADB′=90°,∴B′D=![]() ,
,
∴B′C=3![]() ,
,
在△PCB′中,由勾股定理得:![]() ,解得t=6;
,解得t=6;
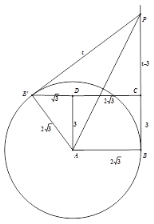
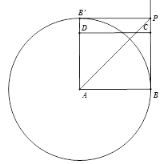
当∠CPB′=90 °时,易得四边形ABPB′为正方形,
∴BP=AB=2![]() ,
,
解得t=2![]() ;
;
综上,t=2或t=6或t=2![]() ;
;
(2)如图
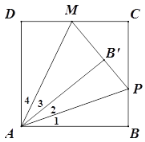
∵∠PAM=45°,
∴∠2+∠3=45°,∠1+∠4=45°,
又∵翻折,
∴∠1=∠2,∠3=∠4,
又∵∠ADM=∠AB′M=90°,AM=AM,
∴△DAM≌△B′AM,
∴AD=AB′=AB,
∴四边形ABCD是正方形,
如图,

设∠APB=x,
∴∠PAB=90°-x,
∴∠DAP=x,
∵AD=AB′,AM=AM,∠ADM=∠AB′M=90°,
∴Rt△MDA≌Rt△B′AM(HL),
∴∠B′AM=∠DAM,
∵翻折,
∴∠PAB=∠PAB′=90°-x,
∴∠DAB′=∠PAB′-∠DAP=90°-2x,
∴∠DAM=![]() ∠DAB′=45°-x,
∠DAB′=45°-x,
∴∠MAP=∠DAM+∠PAD=45°.