Question

【题目】如图，在直角坐标系中，直线y=﹣x与反比例函数y=的图象交于关于原点对称的A，B两点，已知A点的纵坐标是3．

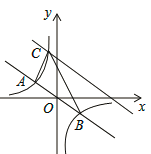
（1）求反比例函数的表达式；

（2）将直线y=﹣x向上平移后与反比例函数在第二象限内交于点C，如果△ABC的面积为48，求平移后的直线的函数表达式．

Answer 1

【答案】（1）y=﹣；（2）y=﹣x+8．

【解析】

试题分析：（1）将y=3代入一次函数解析式中，求出x的值，即可得出点A的坐标，再利用反比例函数图象上点的坐标特征即可求出反比例函数的表达式；（2）根据A、B点关于原点对称，可求出点B的坐标以及线段AB的长度，设出平移后的直线的函数表达式，根据平行线间的距离公式结合三角形的面积即可得出关于b的一元一次方程，解方程即可得出结论．

试题解析：（1）令一次函数y=﹣x中y=3，则3=﹣x， 解得：x=﹣6，即点A的坐标为（﹣6，3）．

∵点A（﹣6，3）在反比例函数y=的图象上， ∴k=﹣6×3=﹣18，

∴反比例函数的表达式为y=﹣．

（2）∵A、B两点关于原点对称， ∴点B的坐标为（6，﹣3）， ∴AB==6．

设平移后的直线的函数表达式为y=﹣x+b（b＞0），即x+2y﹣2b=0，

直线y=﹣x可变形为x+2y=0， ∴两直线间的距离d==b．

∴S△ABC=ABd=×6×b=48， 解得：b=8．

∴平移后的直线的函数表达式为y=﹣x+8．