题目内容
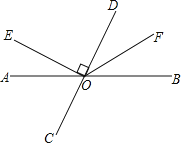
【题目】如图,直线AB、CD相交于点O,OE⊥CD,OF平分∠BOD.
(1)图中除直角外,请写出一对相等的角吗: (写出符合的一对即可)
(2)如果∠AOE=26°,求∠BOD和∠COF的度数.(所求的角均小于平角)
【答案】(1)∠DOF=∠BOF;(2)∠BOD=64°,∠COF=148°.
【解析】试题分析:(1)利用角平分线的性质可得∠DOF=∠BOF;(2)已知OE⊥CD,根据垂直的定义可得∠COE=90°,根据∠AOC=∠COE﹣∠AOE求得∠AOC的度数,根据对顶角相等可得∠AOC=∠BOD,又因OF平分∠BOD,可求得∠DOF的度数,再由∠COF=180°﹣∠DOF即可求得∠COF的度数.
试题解析:
(1)∠DOF=∠BOF
(2)∵OE⊥CD,
∴∠COE=90°,
∴∠AOC=∠COE﹣∠AOE=90°﹣26°=64°,
∵∠AOC=∠BOD,
∴∠BOD=64°,
又∵OF平分∠BOD,
∴∠DOF=![]() ∠BOD=
∠BOD=![]() ×64°=32°,
×64°=32°,
∴∠COF=180°﹣∠DOF=180°﹣32°=148°=148°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目