题目内容
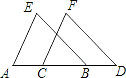
 已知AC=BD,AE=CF,BE=DF,问AE∥CF吗?
已知AC=BD,AE=CF,BE=DF,问AE∥CF吗?
解:AE∥CF.
∵AC=BD,
∴AC+CB=CB+BD.
∴AB=CD.
在△EAB和△FCD中,
∵AE=CF(已知),AB=CD(已证),BE=DF(已知),
∴△EAB≌△FCD(SSS).
∴∠A=∠FCD(全等三角形的对应角相等).
∴AE∥CF(同位角相等,两直线平行).
分析:AB=AC+BC,CD=BD+BC,因为AC=BD,所以AB=CD,又因为AE=CF,BE=DF,则满足△ABE与△CDF全等的条件,全等三角形三个角分别相等,即∠A=∠FCD,满足关于AE∥CF的条件:同位角相等,两直线平行.
点评:本题考查三角形全等的判定及性质定理以及平行线的判定定理.由三角形全等得角相等,从而得到两线平行时一种很常用的方法,注意掌握.
∵AC=BD,
∴AC+CB=CB+BD.
∴AB=CD.
在△EAB和△FCD中,
∵AE=CF(已知),AB=CD(已证),BE=DF(已知),
∴△EAB≌△FCD(SSS).
∴∠A=∠FCD(全等三角形的对应角相等).
∴AE∥CF(同位角相等,两直线平行).
分析:AB=AC+BC,CD=BD+BC,因为AC=BD,所以AB=CD,又因为AE=CF,BE=DF,则满足△ABE与△CDF全等的条件,全等三角形三个角分别相等,即∠A=∠FCD,满足关于AE∥CF的条件:同位角相等,两直线平行.
点评:本题考查三角形全等的判定及性质定理以及平行线的判定定理.由三角形全等得角相等,从而得到两线平行时一种很常用的方法,注意掌握.

练习册系列答案
相关题目
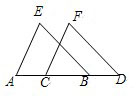 22、已知AC=BD,AE=CF,BE=DF,问AE∥CF吗?
22、已知AC=BD,AE=CF,BE=DF,问AE∥CF吗? 如图,已知AC=BD,AE=BF,CF=DE,请写出图中两对相等的角并证明.
如图,已知AC=BD,AE=BF,CF=DE,请写出图中两对相等的角并证明.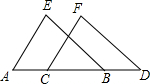 已知AC=BD,AE=CF,
已知AC=BD,AE=CF, 如图,已知AC=BD,AE=CF,AE∥CF,求证:BE=DF.
如图,已知AC=BD,AE=CF,AE∥CF,求证:BE=DF.