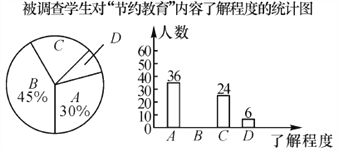
题目内容
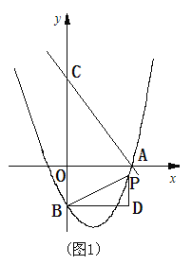
【题目】如图1,直线![]() 交
交![]() 轴于点A,交
轴于点A,交![]() 轴于点C(0,4).抛物线
轴于点C(0,4).抛物线![]() 经过点A,交
经过点A,交![]() 轴于点B(0,-2).点P为抛物线上一个动点,经过点P作
轴于点B(0,-2).点P为抛物线上一个动点,经过点P作![]() 轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为
轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为![]() .
.
(1)求抛物线的解析式;
(2)当△BDP为等腰直角三角形时,求线段PD的长;
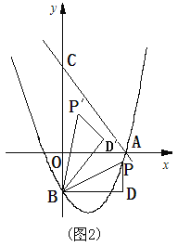
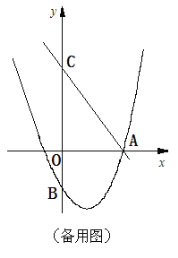
(3)如图2,将△BDP绕点B逆时针旋转,得到△BD′P′,且旋转角∠PBP′=∠OAC,当点P的对应点P′落在坐标轴上时,请直接写出点P的坐标.
【答案】(1)![]() ;
;
(2)当△BPD为等腰直角三角形时,PD的长为![]() .
.
(3)![]() ,
,![]() ,
,![]() .
.
【解析】
试题分析:(1)先求得点A的坐标,再利用待定系数法求抛物线的解析式即可;(2)设点P的横坐标为![]() ,可得P(m,
,可得P(m,![]() ),D(m,-2),若△BPD为等腰直角三角形,则PD=BD.分两种情况:①当点P在直线BD的上方时,PD=
),D(m,-2),若△BPD为等腰直角三角形,则PD=BD.分两种情况:①当点P在直线BD的上方时,PD=![]() ,再分点P在y轴的左侧和右侧两种情况,列方程求解即可;②当点P在直线BD的下方时,m>0,BD=m,PD=
,再分点P在y轴的左侧和右侧两种情况,列方程求解即可;②当点P在直线BD的下方时,m>0,BD=m,PD=![]() ,列方程求解即可;(3)∵∠PBP/=∠OAC,OA=3,OC=4;∴AC=5,∴sin∠PBP/=
,列方程求解即可;(3)∵∠PBP/=∠OAC,OA=3,OC=4;∴AC=5,∴sin∠PBP/=![]() ,cos∠PBP/=
,cos∠PBP/=![]() ,①当点P/落在x轴上时,过点D/作D/N⊥x轴于N,交BD于点M,∠DBD/=∠ND/P/=∠PBP/,如图1,ND/-MD/=2,即
,①当点P/落在x轴上时,过点D/作D/N⊥x轴于N,交BD于点M,∠DBD/=∠ND/P/=∠PBP/,如图1,ND/-MD/=2,即![]() ×(
×(![]() m2-
m2-![]() m)-(-
m)-(-![]() m)=2;如图2,ND/-MD/=2,即
m)=2;如图2,ND/-MD/=2,即![]() ×(
×(![]() m2-
m2-![]() m)-(-
m)-(-![]() m)=2解得:P(-
m)=2解得:P(-![]() ,
,![]() )或P(
)或P(![]() ,
,![]() );②当点P/落在y轴上时,
);②当点P/落在y轴上时,
如图3,过点D/作D/M⊥x轴交BD于点M,过点P/作P/N⊥y轴,交MD/的延长线于点N,∠DBD/=∠ND/P/=∠PBP/,∵PN=BM,即 ![]() ×(
×(![]() m2-
m2-![]() m)=
m)= ![]() m∴P(
m∴P(![]() ,
,![]() )
)
试题解析:(1)由直线![]() 过点C(0,4),得n=4,∴
过点C(0,4),得n=4,∴![]() .
.
当y=0时,![]() ,解得x=3,∴A(3,0).
,解得x=3,∴A(3,0).
∵抛物线![]() 经过点A(3,0),B(0,-2),
经过点A(3,0),B(0,-2),
∴ ,解得
,解得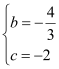
∴![]() .
.
(2)设点P的横坐标为![]() ,∴P(m,
,∴P(m,![]() ),D(m,-2).
),D(m,-2).
若△BPD为等腰直角三角形,则PD=BD.
①当点P在直线BD的上方时,PD=![]() ,
,
(Ⅰ)若点P在y轴的左侧,则m<0,BD=-m,
∴![]() ,
,
解得![]() (舍去).
(舍去).
(Ⅱ)若点P在y轴的右侧,则m>0,BD=m,
∴![]() ,
,
解得![]() .
.
②当点P在直线BD的下方时,m>0,BD=m,PD=![]() ,
,
∴![]() ,
,
解得![]() .
.
综上m=![]() .
.
即当△BPD为等腰直角三角形时,PD的长为![]() .
.
(3)![]() ,
,![]() ,
,![]() .
.