Question

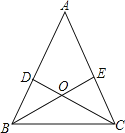
【题目】如图所示，在△ABC中，AB=AC，∠A=36°，两条角平分线BE、CD相交于点O，则图中等腰三角形有（ ）

A．3个 B．5个 C．7个 D．8个

Answer 1

【答案】D

【解析】

试题分析：由AB=AC，∠A=36°，CD、BE是△ABC的角平分线，可求得∠ABE=∠CBE=∠ACD=∠BCD=∠A=36°，即可得△ABC，△ABE，△ACD，△BOC是等腰三角形，然后由三角形内角和定理与三角形外角的性质，可求得∠BEC=∠BDC=∠ABC=∠ACB=∠BOD=∠COE=72°，继而可得△BOD，△COE，△BCE，△CBD是等腰三角形．

解：∵在△ABC中，AB=AC，∠A=36°，

∴∠ABC=∠ACB==72°，

∵CD、BE是△ABC的角平分线，

∴∠ABE=∠CBE=∠ACD=∠BCD=∠A=36°，

∴AE=BE，AD=CD，OB=OC，

∴△ABC，△ABE，△ACD，△BOC是等腰三角形，

∵∠BEC=180°﹣∠ACB﹣∠CBE=72°，∠CDB=180°﹣∠ABC﹣∠BCD=72°，∠BOD=∠COE=∠CBE+∠BCD=72°，

∴∠BEC=∠BDC=∠ABC=∠ACB=∠BOD=∠COE=72°，

∴BD=OB，OC=CE，BC=BE=CD，

∴△BOD，△COE，△BCE，△CBD是等腰三角形．

∴图中的等腰三角形有8个．

故选D．