题目内容
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象经过一次函数y=-![]() x+3的图象与x轴、y轴的交点,并且也经过(1,1)点,求这个二次函数的关系式,并求x为何值时,函数有最大(最小)值?这个值是多少?
x+3的图象与x轴、y轴的交点,并且也经过(1,1)点,求这个二次函数的关系式,并求x为何值时,函数有最大(最小)值?这个值是多少?
【答案】二次函数的关系式为y=![]() x2-
x2-![]() x+3,当x=
x+3,当x=![]() 时,函数有最小值,最小值为-
时,函数有最小值,最小值为-![]() .
.
【解析】
先求出一次函数y=-![]() x+3的图象与x轴、y轴的交点,再把这三点代入二次函数y=ax2+bx+c,求出解析式,再把解析式化成顶点式,即可得当x取何值时有最值.
x+3的图象与x轴、y轴的交点,再把这三点代入二次函数y=ax2+bx+c,求出解析式,再把解析式化成顶点式,即可得当x取何值时有最值.
解:对于y=-![]() x+3,当x=0时,y=3;当y=0时,x=2,把(0,3),(2,0),(1,1)分别代入y=ax2+bx+c,得
x+3,当x=0时,y=3;当y=0时,x=2,把(0,3),(2,0),(1,1)分别代入y=ax2+bx+c,得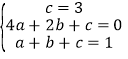 ,
,
所以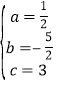 ,
,
所以二次函数的关系式为y=![]() x2-
x2-![]() x+3.
x+3.
因为y=![]() x2-
x2-![]() x+3=
x+3=![]() (x-
(x-![]() )-
)-![]() ,所以当x=
,所以当x=![]() 时,函数有最小值,最小值为-
时,函数有最小值,最小值为-![]() .
.

练习册系列答案
相关题目