题目内容
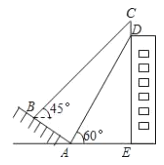
【题目】如图,小华和小康想用标杆来测量河对岸的树AB的高,两人在确保无安全隐患的情况下,小康在F处竖立了一根标杆EF,小华走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上,此时测得小华的眼睛到地面的距离DC=16米;然后,小华在C处蹲下,小康平移标杆到H处时,小华恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小华的眼睛到地面的距离MC=0.8米.已知EF=GH=2.4米,CF=2米,FH=1.6米,点C、F、H、A在一条直线上,点M在CD上,CD⊥AC,EF⊥AC,CH⊥AC,AB⊥AC,根据以上测量过程及测量数据,请你求出树AB的高度.
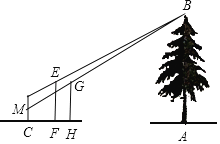
【答案】树AB的高度为8.8米.
【解析】
根据相似三角形的性质得方程,解方程组即可得到结论.
解:过点D作DP⊥AB于点P,交EF于点N,过点M作MQ⊥AB于点Q,交GH于点K,
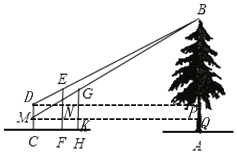
由题意可得:∠EDN=∠BDP,∠BPD=∠END,∠GMK=∠BMQ
∠BQM=∠GKM,DP=MQ=AC,DN=CF,MK=CH,
∴△DEN∽△DBP,△GMK∽△BMQ,
∴![]()
∴![]()
∴AB=8.8米
∴树AB的高度为8.8米.

练习册系列答案
相关题目