Question

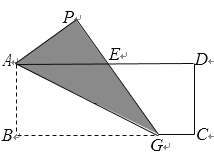
【题目】如图，矩形纸片ABCD中，AB=4，BC=10，G是BC边上一点，沿AG折叠△ABG，点B的落点为P，GP交AD于点E. 若E是AD的中点，则BG的长是_______.

Answer 1

【答案】8

【解析】

根据矩形的性质得到AD∥BC，由折叠的性质得到△ABG≌△APG，进而得到△AEG为等腰三角形，则BG=PG=PE+EG=PE+AE，由勾股定理可求得PE长，即可得出答案.

∵四边形ABCD为矩形，

∴AD∥BC，

∴∠EAG=∠AGB，

由折叠性质可得△ABG≌△APG，

∴∠AGB=∠AGP，

∴∠EAG=∠AGP，即△AEG为等腰三角形，

∴AE=EG，

∵AB=4，BC=10，E为AD中点，

∴AP=4，AE=5，

∴PE=3，

∴BG=PG= PE+EG=PE+AE=8，

故答案为：8.