题目内容
已知二次函数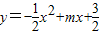 的图象经过点A(-3,-6),并且该抛物线与x轴交于B、C两点,与y轴的交点为E,P为抛物线的顶点.如图所示.
的图象经过点A(-3,-6),并且该抛物线与x轴交于B、C两点,与y轴的交点为E,P为抛物线的顶点.如图所示.(1)求这个二次函数表达式.
(2)设点D为线段OC上的一点,且满足∠DPC=∠BAC,说明直线PC与直线AC的位置关系,并求出点D的坐标.
(3)在(1)中的抛物线上是否存在一点F,使S△BCF=
 S△BCP?若存在,请直接写出F点的坐标;若不存在,请说明理由.
S△BCP?若存在,请直接写出F点的坐标;若不存在,请说明理由.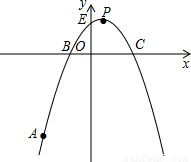
【答案】分析:(1)把A点坐标代入二次函数 可求出m,从而确定二次函数的解析式;
可求出m,从而确定二次函数的解析式;
(2)先把二次函数配成顶点式得到顶点P的坐标为(1,2),设点D坐标为(a,0),过点P作PH⊥x轴,垂足为H,过点A作AQ⊥x轴,垂足为Q,根据点的坐标可得到
△PCH和△AQC都是等腰直角三角形,则∠PCH=45°,∠ACQ=45°,于是得到直线PC与直线AC垂直;由∠DPC=∠BAC,∠PCD=∠ACB得到△PDC∽Rt△ABC,根据相似比有
 =
= ,即
,即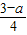 =
= ,解得a=
,解得a= ,从而得到D点坐标;
,从而得到D点坐标;
(3)先计算出S△BCP=4,则S△BCF= S△BCP=3,设F点坐标为(x,y),则
S△BCP=3,设F点坐标为(x,y),则 ×4×|y|=3,解得y=
×4×|y|=3,解得y= 或-
或- ,然后分别代入二次函数解析式中求出对应的x的值,从而得到F点的坐标.
,然后分别代入二次函数解析式中求出对应的x的值,从而得到F点的坐标.
解答:解:(1) ∵点A(-3,-6)在抛物线上,
∵点A(-3,-6)在抛物线上,
∴-6=- ×9-3m+
×9-3m+ ,
,
解得m=1,
∴所求二次函数的表达式为y=- x2+x+
x2+x+ ;
;
(2)∵y=- x2+x+
x2+x+ =-
=- (x-1)2+2,
(x-1)2+2,
∴P点坐标为(1,2),
如图,设点D坐标为(a,0),过点P作PH⊥x轴,垂足为H,
过点A作AQ⊥x轴,垂足为Q,
令y=0得- x2+x+
x2+x+ =0,解得x1=-1,x2=3,
=0,解得x1=-1,x2=3,
∴B点坐标为(-1,0),C点坐标为(3,0)
∵P(1,2),A(-3,-6),
∴PH=HC=2,QA=QC=6,
∴△PCH和△AQC都是等腰直角三角形,
∴∠PCH=45°,∠ACQ=45°,
∴∠PCA=90°,
∴PC⊥CA;
∵∠DPC=∠BAC,∠PCD=∠ACB,
∴△PDC∽Rt△ABC,
∴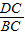 =
=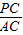 ,即
,即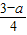 =
=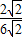 ,解得a=
,解得a= ,
,
∴D坐标为( ,0);
,0);
(3)存在.
∵S△BCP= ×4×2=4,
×4×2=4,
而S△BCF= S△BCP,
S△BCP,
∴S△BCF=3,
设F点坐标为(x,y)
∴ ×4×|y|=3,
×4×|y|=3,
∴y= 或-
或- ,
,
当y= 时,-
时,- x2+x+
x2+x+ =
= ,解得x1=0,x2=2;
,解得x1=0,x2=2;
当y=- 时,-
时,- x2+x+
x2+x+ =-
=- ,解得x1=1+
,解得x1=1+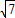 ,x2=1-
,x2=1-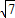 ,
,
∴F(0, )或(2,
)或(2, )或(1+
)或(1+ ,-
,- )或(1-
)或(1-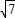 ,-
,- ).
).
点评:本题考查了二次函数的综合题:先根据几何条件确定抛物线上点的坐标,再利用待定系数法确定抛物线的解析式,然后运用二次函数的性质解决有关问题.
 可求出m,从而确定二次函数的解析式;
可求出m,从而确定二次函数的解析式;(2)先把二次函数配成顶点式得到顶点P的坐标为(1,2),设点D坐标为(a,0),过点P作PH⊥x轴,垂足为H,过点A作AQ⊥x轴,垂足为Q,根据点的坐标可得到
△PCH和△AQC都是等腰直角三角形,则∠PCH=45°,∠ACQ=45°,于是得到直线PC与直线AC垂直;由∠DPC=∠BAC,∠PCD=∠ACB得到△PDC∽Rt△ABC,根据相似比有
 =
= ,即
,即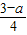 =
= ,解得a=
,解得a= ,从而得到D点坐标;
,从而得到D点坐标;(3)先计算出S△BCP=4,则S△BCF=
 S△BCP=3,设F点坐标为(x,y),则
S△BCP=3,设F点坐标为(x,y),则 ×4×|y|=3,解得y=
×4×|y|=3,解得y= 或-
或- ,然后分别代入二次函数解析式中求出对应的x的值,从而得到F点的坐标.
,然后分别代入二次函数解析式中求出对应的x的值,从而得到F点的坐标.解答:解:(1)
 ∵点A(-3,-6)在抛物线上,
∵点A(-3,-6)在抛物线上,∴-6=-
 ×9-3m+
×9-3m+ ,
,解得m=1,
∴所求二次函数的表达式为y=-
 x2+x+
x2+x+ ;
;(2)∵y=-
 x2+x+
x2+x+ =-
=- (x-1)2+2,
(x-1)2+2,∴P点坐标为(1,2),
如图,设点D坐标为(a,0),过点P作PH⊥x轴,垂足为H,
过点A作AQ⊥x轴,垂足为Q,
令y=0得-
 x2+x+
x2+x+ =0,解得x1=-1,x2=3,
=0,解得x1=-1,x2=3,∴B点坐标为(-1,0),C点坐标为(3,0)
∵P(1,2),A(-3,-6),
∴PH=HC=2,QA=QC=6,
∴△PCH和△AQC都是等腰直角三角形,
∴∠PCH=45°,∠ACQ=45°,
∴∠PCA=90°,
∴PC⊥CA;
∵∠DPC=∠BAC,∠PCD=∠ACB,
∴△PDC∽Rt△ABC,
∴
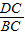 =
=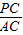 ,即
,即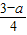 =
=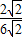 ,解得a=
,解得a= ,
,∴D坐标为(
 ,0);
,0);(3)存在.
∵S△BCP=
 ×4×2=4,
×4×2=4,而S△BCF=
 S△BCP,
S△BCP,∴S△BCF=3,
设F点坐标为(x,y)
∴
 ×4×|y|=3,
×4×|y|=3,∴y=
 或-
或- ,
,当y=
 时,-
时,- x2+x+
x2+x+ =
= ,解得x1=0,x2=2;
,解得x1=0,x2=2;当y=-
 时,-
时,- x2+x+
x2+x+ =-
=- ,解得x1=1+
,解得x1=1+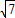 ,x2=1-
,x2=1-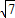 ,
,∴F(0,
 )或(2,
)或(2, )或(1+
)或(1+ ,-
,- )或(1-
)或(1-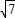 ,-
,- ).
).点评:本题考查了二次函数的综合题:先根据几何条件确定抛物线上点的坐标,再利用待定系数法确定抛物线的解析式,然后运用二次函数的性质解决有关问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目