Question

【题目】小帆同学根据函数的学习经验，对函数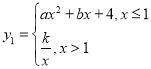进行探究，已知函数过，，．

（1）求函数解析式；

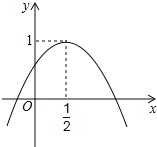
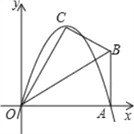
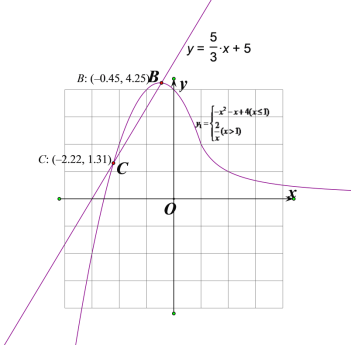
（2）如图1，在平面直角坐标系中画的图象，根据函数图象，写出函数的一条性质　　　　；

（3）结合函数图象回答下列问题：

①方程的近似解的取值范围(精确到个位)是　　　　；

②若一次函数与有且仅有两个交点，则的取值范围是　　　　．

Answer 1

【答案】（1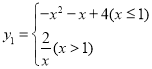）；（2）图象见详解，当时，函数有最大值，函数无最小值；（3）①或；②或．

【解析】

（1）根据待定系数法，即可求解；

（2）画出反比例函数图象和二次函数的图象，即可得到函数的性质；

（3）①画出函数y1与y=的图象，它们的交点的横坐标，就是方程的解，进而即可得到解的取值范围；

②结合一次函数与的图象，即可求解．

（1）将点，代入，

可得，解得，

∴，

将点代入，

可得，解得，

∴，

∴；

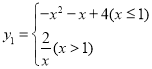（2）函数图象如图所示，由图象可知：当时，函数有最大值，函数无最小值，

故答案是：当时，函数有最大值，函数无最小值；

（3）①画出y=的图象，可得函数y1与y=的图象的交点位置，如图所示，

∴方程的近似解的取值范围(精确到个位)是：或，

故答案是：或；

②由题意可知：的图象过点(0，2)，

当k＞0时，一次函数与有且仅有两个交点，

当的图象与的图象相切时，一次函数与有且仅有两个交点，

∴=有两个相等的根，即：=，

∴k=，

综上所述：或．

故答案是：或．