题目内容
如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.
(1)求证:AD平分∠BAC;
(2)若BE=2,BD=4,求⊙O的半径.

【答案】
(1)证明:连接OD,

∵BC是⊙O的切线,∴OD⊥BC。
又∵AC⊥BC,∴OD∥AC。∴∠2=∠3。
∵OA=OD,∴∠1=∠3。∴∠1=∠2。
∴AD平分∠BAC。
(2)解:∵BC与圆相切于点D,∴BD2=BE•BA。
∵BE=2,BD=4,∴BA=8。
∴AE=AB﹣BE=6。∴⊙O的半径为3。
【解析】切线的性质,平行的性质,切割线定理。
(1)先连接OD,杂而OD⊥BC和AC⊥BC,再由其平行从而得证;
(2)利用切割线定理可先求出AB,进而求出圆的直径,半径则可求出。
【没有学习切割线定理的可连接DE,证△ABD∽△DBE,得AB:BD=BD:BE求得AB=8,···】

练习册系列答案
相关题目
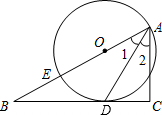 如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D,∠B=30°.求证:
如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D,∠B=30°.求证: (2012•湛江) 如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.
(2012•湛江) 如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.