题目内容
如图，已知点E在直角△ABC的斜边AB上，以AE为直径的⊙O与直角边BC相切于点D．（1）若∠1=30°，∠BAC=
60
60
度；（2）若BE=2，BD=4，则⊙O的半径是：
3
3
．分析：（1）连接OD、DE，根据切线性质得出∠3+∠ADC=90°，求出∠ADC，求出∠2，即可求出答案；
（2）求出∠4=∠1，证△BED∽△BDA，即可求出BA，求出半径即可．
（2）求出∠4=∠1，证△BED∽△BDA，即可求出BA，求出半径即可．
解答：解：（1）连接OD，
∵CD是⊙O切线，
∴∠3+∠ADC=90°，
∵OA=OD，
∴∠1=∠3=30°，
∴∠ADC=60°，
∵∠C=90°，
∴∠2=90°-∠ADC=30°，
∴∠BAC=30°+30°=60°，
故答案为：60；
（2）连接DE，
∵AE为⊙O直径，
∴∠6+∠3=90°，
∵BC为切线，
∴∠4+∠6=90°，
∴∠4=∠3，
∵∠1=∠3，
∴∠4=∠1，
∵∠B=∠B，
∴△BED∽△BDA，
∴
=
，
∴
=
，
∴BA=8，
∴AE=8-2=6，
即⊙O的半径是3，
故答案为：3．
∵CD是⊙O切线，
∴∠3+∠ADC=90°，
∵OA=OD，
∴∠1=∠3=30°，
∴∠ADC=60°，
∵∠C=90°，
∴∠2=90°-∠ADC=30°，
∴∠BAC=30°+30°=60°，
故答案为：60；
（2）连接DE，
∵AE为⊙O直径，
∴∠6+∠3=90°，
∵BC为切线，
∴∠4+∠6=90°，
∴∠4=∠3，
∵∠1=∠3，
∴∠4=∠1，
∵∠B=∠B，
∴△BED∽△BDA，
∴
| BD |
| BE |
| BA |
| BD |
∴
| 4 |
| 2 |
| BA |
| 4 |
∴BA=8，
∴AE=8-2=6，
即⊙O的半径是3，
故答案为：3．
点评：本题考查了切线的性质，相似三角形的性质和判定，等腰三角形的性质的应用，主要考查学生的推理能力．
练习册系列答案
相关题目
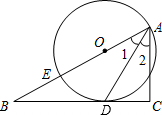如图，已知点E在直角△ABC的斜边AB上，以AE为直径的⊙O与直角边BC相切于点D，∠B=30°．求证：
，求B E的长．