题目内容
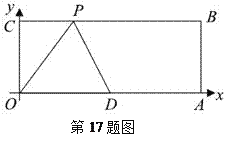
【题目】在平面直角坐标系xOy中,直线y=2x+m与y轴交于点A,与直线y=﹣x+4交于点B(3,n),P为直线y=﹣x+4上一点.
(1)求m,n的值;
(2)在平面直角坐标系系xOy中画直线y=2x+m和直线y=﹣x+4;
(3)当线段AP最短时,求点P的坐标.
【答案】(1)m=﹣5;(2)详见解析;(3)![]()
【解析】
(1)首先把点B(3,n)代入直线y=﹣x+4得出n的值,再进一步代入直线y=2x+m求得m的值即可;(2)根据两点法画一次函数图形即可;(3)过点A作直y=﹣x+4的垂线,垂足为P,进一步利用等腰直角三角形的性质和(1)中与y轴交点的坐标特征解决问题.
解:(1)∵点B(3,n)在直线上y=﹣x+4,
∴n=1,B(3,1)
∵点B(3,1)在直线上y=2x+m上,
∴m=﹣5.
(2)在坐标系中画出y=2x﹣5,y=﹣x+4,如图①,

(3)过点A作直线y=﹣x+4的垂线,垂足为P,如图②
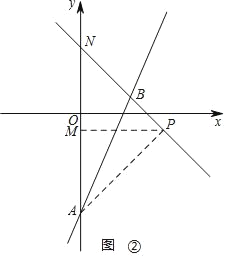 ,
,
此时线段AP最短.
∴∠APN=90°,
∵直线y=﹣x+4与y轴交点N(0,4),直线y=2x﹣5与y轴交点A(0,﹣5),
∴AN=9,∠ANP=45°,
∴AM=PM=![]() ,
,
∴OM=![]()
∴![]() .
.

练习册系列答案
相关题目