题目内容
如图,已知二次函数的图象经过点A(6,0)、B(﹣2,0)和点C(0,﹣8).
(1)求该二次函数的解析式;
(2)设该二次函数图象的顶点为M,若点K为x轴上的动点,当△KCM的周长最小时,点K的坐标为 ![]() ;
;
(3)连接AC,有两动点P、Q同时从点O出发,其中点P以每秒3个单位长度的速度沿折线OAC按O→A→C的路线运动,点Q以每秒8个单位长度的速度沿折线OCA按O→C→A的路线运动,当P、Q两点相遇时,它们都停止运动,设P、Q同时从点O出发t秒时,△OPQ的面积为S.
①请问P、Q两点在运动过程中,是否存在PQ∥OC?若存在,
请求出此时t的值;若不存在,请说明理由;
②请求出S关于t的函数关系式,并写出自变量t的取值范围;
③设S0是②中函数S的最大值,直接写出S0的值.

解:(1)设二次函数的解析式为y=a(x+2)(x﹣6)
∵图象过点(0,﹣8)
∴a=![]()
∴二次函数的解析式为y=![]() x2﹣
x2﹣![]() x﹣8;--------------------(2分)
x﹣8;--------------------(2分)
(2)∵y=![]()
![]() x2﹣
x2﹣![]() x﹣8=
x﹣8=![]() (x2﹣4x+4﹣4)﹣8=
(x2﹣4x+4﹣4)﹣8=![]() (x﹣2)2﹣
(x﹣2)2﹣![]()
∴点M的坐标为(2,﹣![]() )
)
∵点C的坐标为(0,﹣8),
∴点C关于x轴对称的点C′的坐标为(0,8)
∴直线C′M的解析式为:y=﹣![]() x+8
x+8
令y=0
得﹣![]() x+8=0
x+8=0
解得:x=![]()
∴点K的坐![]() 标为(
标为(![]() ,0);-------------------(2分)
,0);-------------------(2分)
(3)①不存在PQ∥OC,
若PQ∥OC,则点P,Q分别在线段OA,CA上,
此时,1<t<2
∵PQ∥OC,
∴△APQ∽△AOC
∴![]()
∵AP=6﹣3t
AQ=18﹣8t,
∴![]()
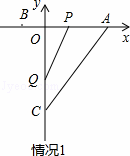
∴t=![]()
∵t=![]() >2不满足1<t<2;
>2不满足1<t<2;
∴不存在PQ∥OC;-----------------------(3分)

③当0≤t≤1时,S=12t2,函数的最大值是12;
当1<t≤2时,S=﹣![]() +
+![]() ,函数的最大值是
,函数的最大值是![]() ;
;
当2<t<![]() ,S=
,S=![]() QP•OF=﹣
QP•OF=﹣![]() +
+![]() ,函数的最大值为
,函数的最大值为![]() ;-------------(3分)
;-------------(3分)
∴S0的值为![]() -----------------(2分).
-----------------(2分).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.
的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C. (2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).
(2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).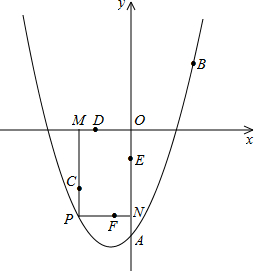 (2013•常德)如图,已知二次函数的图象过点A(0,-3),B(
(2013•常德)如图,已知二次函数的图象过点A(0,-3),B( 如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4).
如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4). 如图,已知二次函数的图象(0≤x≤3.4),关于该函数在所给自变量的取值范围内,下列说法正确的是( )
如图,已知二次函数的图象(0≤x≤3.4),关于该函数在所给自变量的取值范围内,下列说法正确的是( )