题目内容
【题目】如图，在菱形ABCD中，边长为1，∠A=60°，顺次连结菱形ABCD各边中点，可得四边形A1B1C1D1；顺次连结四边形A1B1C1D1各边中点，可得四边形A2B2C2D2；顺次连结四边形A2B2C2D2各边中点，可得四边形A3B3C3D3；按此规律继续下去…，则四边形A2016B2016C2016D2016的面积是 ．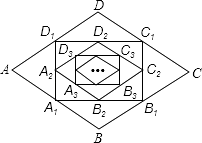 
【答案】
【解析】解：如图，连接AC、BD．则AC⊥BD．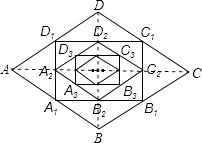 
∵菱形ABCD中，边长为1，∠A=60°，
∴S菱形ABCD= 
ACBD=1×1×sin60°= 
∵顺次连结菱形ABCD各边中点，可得四边形A1B1C1D1 ，
易证四边形A1B1C1D1 是矩形，
S矩形A1B1C1D1= C BD= 
ACBD= S菱形ABCD ．
同理，S四边形A2B2C2D2= S矩形A1B1C1D1= S菱形ABCD ，
S矩形A3B3C3D3=（ ）3S菱形ABCD ．
四边形A2016B2016C2016D2016的面积是= 
S菱形ABCD= ，
所以答案是： ．
【考点精析】利用菱形的性质对题目进行判断即可得到答案，需要熟知菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】为建设秀美龙江，某学校组织师生参加一年一度的植树绿化工作，准备租用7辆客车，现有甲、乙两种客车，它们的载客量和租金如下表，设租用甲种客车x辆，租车总费用为y元，
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 60 | 40 |
租金/(元/辆) | 360 | 300 |
（1）求出y（单位：元）与x（单位：辆）之间的函数关系式。
（2）若该校共有350名师生前往参加劳动，共有多少种租车方案？
（3）带队老师从学校预支租车费用2400元，试问预支的租车费用是否可有结余？若有结余，最多可结余多少元。
