题目内容
在直角三角形ABC中,已知两边分别6和8,D、E分别是两条直角边上的中点,则线段DE长是
- A.3
- B.4
- C.5
- D.5或4
D
分析:根据已知D、E分别是两条直角边上的中点,得出DE是直角三角形斜边上的中位线,求出斜边长即可得出DE的长.
解答: 解:∵直角三角形ABC中,两边分别6和8,
解:∵直角三角形ABC中,两边分别6和8,
∴当AC=8,AB=6,
∴BC=10,
∵D、E分别是两条直角边上的中点,
∴DE∥BC,且DE= BC,
BC,
∴DE=5,
当BC=8,
∵D、E分别是两条直角边上的中点,
∴DE∥BC,且DE= BC,
BC,
∴DE=4,
则线段DE长是5或4,
故选:D.
点评:此题考查了三角形的中位线定理,根据三角形的两边分别6和8,进行分类讨论再利用三角形的中位线性质定理求出是解决问题的关键.
分析:根据已知D、E分别是两条直角边上的中点,得出DE是直角三角形斜边上的中位线,求出斜边长即可得出DE的长.
解答:
 解:∵直角三角形ABC中,两边分别6和8,
解:∵直角三角形ABC中,两边分别6和8,∴当AC=8,AB=6,
∴BC=10,
∵D、E分别是两条直角边上的中点,
∴DE∥BC,且DE=
 BC,
BC,∴DE=5,
当BC=8,
∵D、E分别是两条直角边上的中点,
∴DE∥BC,且DE=
 BC,
BC,∴DE=4,
则线段DE长是5或4,
故选:D.
点评:此题考查了三角形的中位线定理,根据三角形的两边分别6和8,进行分类讨论再利用三角形的中位线性质定理求出是解决问题的关键.

练习册系列答案
相关题目
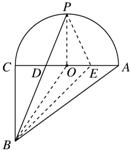 6、如图,在直角三角形ABC中,∠ACB=90°,CA=4,点P是半圆弧AC的中点,连接BP,线段即把图形APCB(指半圆和三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是
6、如图,在直角三角形ABC中,∠ACB=90°,CA=4,点P是半圆弧AC的中点,连接BP,线段即把图形APCB(指半圆和三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是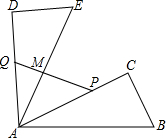 使点B落在点E处,点C落在点D处.P、Q分别为线段AC、AD上的两个动点,且AQ=2PC,连接PQ交线段AE于点M.
使点B落在点E处,点C落在点D处.P、Q分别为线段AC、AD上的两个动点,且AQ=2PC,连接PQ交线段AE于点M.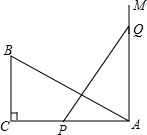 如图,在直角三角形ABC中,∠C=90°,AC=20,BC=10,PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动,且点P不与点A,C重合,那么当点P运动到什么位置时,才能使△ABC与△APQ全等?
如图,在直角三角形ABC中,∠C=90°,AC=20,BC=10,PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动,且点P不与点A,C重合,那么当点P运动到什么位置时,才能使△ABC与△APQ全等?