题目内容
【题目】已知,如图1, ![]() 分别为定角(大小不会发生改变)
分别为定角(大小不会发生改变) ![]() 内部的两条动射线,
内部的两条动射线,![]() 与
与 ![]() 互补,
互补,![]() .
.
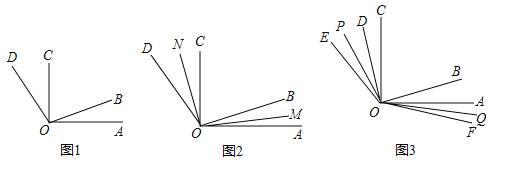
(1)求![]() 的度数:
的度数:
(2)如图2,射线![]() 分别为
分别为![]() 的平分线,当
的平分线,当![]() 绕着点
绕着点![]() 旋转时,下列结论:①
旋转时,下列结论:①![]() 的度数不变:②
的度数不变:②![]() 的度数不变,其中只有一个是正确的,请你做出正确的选择并求值:
的度数不变,其中只有一个是正确的,请你做出正确的选择并求值:
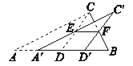
(3)如图3, ![]() 是
是![]() 外部的两条射线,且
外部的两条射线,且![]() ,
, ![]()
![]() ,当
,当![]() 绕着点
绕着点![]() 旋转时,
旋转时,![]() 的大小是否会发生变化?若不变,求出其度数:若变化,说明理由,
的大小是否会发生变化?若不变,求出其度数:若变化,说明理由,
【答案】(1)![]() ;(2)②正确,
;(2)②正确,![]() 的度数为90°不变;(3)
的度数为90°不变;(3) ![]() 的大小不变为130° ,
的大小不变为130° ,
【解析】
(1)根据角的定义可知∠AOC+∠BOD=180°,与∠AOB+∠COD=50°,结合可得∠BOC的度数,即可求出∠AOD的度数;
(2)根据角平分线的定义得出∠MON=∠CON+∠BOM+∠BOC=25°+65°=90°;
(3)先求得∠DOE+∠AOF的值,再根据角平分线的定义得出∠POD+∠AOQ,再加上∠AOD即可得∠POQ的值.
解: (1)∵![]() 互补,
互补,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)②正确,![]() 的度数为90°不变;理由如下: .
的度数为90°不变;理由如下: .
∵![]() 的平分线,
的平分线,
∴![]() ,
,
∴![]() ,
,
故②正确,![]() 的度数为90°不变;
的度数为90°不变;
(3) ![]() 的大小不变为130° ,
的大小不变为130° ,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()

练习册系列答案
相关题目