题目内容
【题目】如图,在△ABC中,以BC为直径的圆交AC于点D,∠ABD=∠ACB. 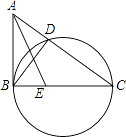
(1)求证:AB是圆的切线;
(2)若点E是BC上一点,已知BE=4,tan∠AEB= ![]() ,AB:BC=2:3,求圆的直径.
,AB:BC=2:3,求圆的直径.
【答案】
(1)证明:∵BC是直径,
∴∠BDC=90°,
∴∠ACB+∠DBC=90°,
∵∠ABD=∠ACB,
∴∠ABD+∠DBC=90°
∴∠ABC=90°
∴AB⊥BC,
∴AB是圆的切线
(2)解:在RT△AEB中,tan∠AEB= ![]() ,
,
∴ ![]() =
= ![]() ,即AB=
,即AB= ![]() BE=
BE= ![]() ,
,
在RT△ABC中, ![]() =
= ![]() ,
,
∴BC= ![]() AB=10,
AB=10,
∴圆的直径为10
【解析】(1)欲证明AB是圆的切线,只要证明∠ABC=90°即可.(2)在RT△AEB中,根据tan∠AEB= ![]() ,求出BC,在RT△ABC中,根据
,求出BC,在RT△ABC中,根据 ![]() =
= ![]() 求出AB即可.
求出AB即可.
【考点精析】关于本题考查的切线的判定定理,需要了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能得出正确答案.

练习册系列答案
相关题目