Question

【题目】如图，把Rt△ACO以O点为中心，逆时针旋转90°，得Rt△BDO，点B坐标为（0，﹣3），点C坐标为（0， ），抛物线y=﹣ x2+bx+c经过点A和点C．

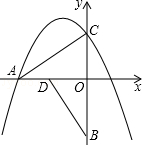
（1）求b，c的值；
（2）在x轴以上的抛物线对称轴上是否存在点Q，使得△ACQ为等腰三角形？若存在，直接写出点Q的坐标；若不存在，请说明理由
（3）点P从点O出发沿x轴向负半轴运动，每秒1个单位，过点P作y轴的平行线交抛物线于点M，当t为几秒时，以M、P、O、C为顶点得四边形是平行四边形？

Answer 1

【答案】
（1）

解：由旋转知：OA=OB=3．

∴A（﹣3，0）．

由 ，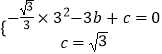

∴ ；

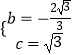（2）

解：存在，有2个Q点，坐标分别为：（﹣1， ）；（﹣1， ）．

解答如下：设Q（﹣1，t）．

∵A（﹣3，0），C（0， ），

∴AC= =2 ．

①当AC=AQ时，2 = ，

解得t=2 ，即Q（﹣1， ）；

②当AC=CQ时，2 = ，

解得t= ，即Q（﹣1， ）．

（3）

解：∵OC= ，当 M、P、O、C为顶点得四边形是平行四边形时，PM=

∴M点的纵坐标为 或﹣ ．

由

解之，x=﹣2或0

由 ，

解之，x=﹣1+ 或﹣1﹣ ．

结合条件及图形分析得：OP=2或 +1，

∴当t=2或 +1秒时，以M、P、O、C为顶点得四边形是平行四边形．

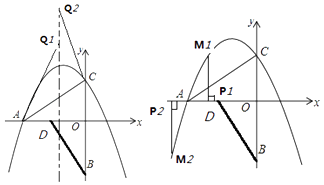
【解析】（1）由旋转的性质得OA=OB=3，从而得到点A的坐标，把点A、C的坐标分别代入函数解析式，然后利用待定系数法求b，c的值；（2）根据题意作出图形，结合图形易得点Q的坐标；（3）根据平行四边形的对边相等的性质和坐标与图形的性质进行解答．