题目内容
设一次函数y=k1x+b1(k1≠0),y=k2x+b2(k2≠0),则称函数y=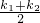 x+
x+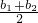 为此两个函数的平均函数.
为此两个函数的平均函数.
(1)若一次函数y=ax+1,y=-4x+3的平均函数为y=3x+2,求a的值;
(2)若由一次函数y=x+1,y=kx+1的图象与x轴围成的三角形面积为1,求这两个函数的平均函数.
解:(1)根据题意得 ,解得a=10;
,解得a=10;
(2)如图,直线y=x+1与坐标轴交于(0,1),(-1,0),而直线y=k x+1经过点(0,1),交x轴于点(- ,0)),
,0)),
∴ |-1+
|-1+ |×1=1,解得k=
|×1=1,解得k= 或-1,
或-1,
∴两个函数的平均函数为y= x+1或y=1.
x+1或y=1.
分析:(1)根据新定义得到 ,然后解方程;
,然后解方程;
(2)先根据三角形面积公式求出k的值,然后根据新定义求解.
点评:本题考查了一次函数图象的性质:一次函数y=kx+b(k、b为常数,k≠0)是一条直线,当k>0,图象经过第一、三象限,y随x的增大而增大;当k<0,图象经过第二、四象限,y随x的增大而减小;图象与y轴的交点坐标为(0,b).
 ,解得a=10;
,解得a=10;
(2)如图,直线y=x+1与坐标轴交于(0,1),(-1,0),而直线y=k x+1经过点(0,1),交x轴于点(-
 ,0)),
,0)),∴
 |-1+
|-1+ |×1=1,解得k=
|×1=1,解得k= 或-1,
或-1,∴两个函数的平均函数为y=
 x+1或y=1.
x+1或y=1.分析:(1)根据新定义得到
 ,然后解方程;
,然后解方程;(2)先根据三角形面积公式求出k的值,然后根据新定义求解.
点评:本题考查了一次函数图象的性质:一次函数y=kx+b(k、b为常数,k≠0)是一条直线,当k>0,图象经过第一、三象限,y随x的增大而增大;当k<0,图象经过第二、四象限,y随x的增大而减小;图象与y轴的交点坐标为(0,b).

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 双曲线
双曲线 我们就称直线l1与直线l2互相平行.解答下面的问题:
我们就称直线l1与直线l2互相平行.解答下面的问题: 设一次函数y=k1x+b1(k1≠0)的图象为l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.解答下面的问题:
设一次函数y=k1x+b1(k1≠0)的图象为l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.解答下面的问题: 阅读下面的材料:
阅读下面的材料: