题目内容
【题目】△OPA和△OQB分别是以OP、OQ为直角边的等腰直角三角形,点C、D、E分别是OA、OB、AB的中点.
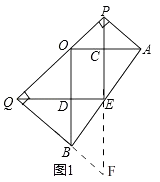
(1)当∠AOB=90°时如图1,连接PE、QE,直接写出EP与EQ的大小关系;
(2)将△OQB绕点O逆时针方向旋转,当∠AOB是锐角时如图2,(1)中的结论是否成立?若成立,请给出证明;若不成立,请加以说明.
(3)仍将△OQB绕点O旋转,当∠AOB为钝角时,延长PC、QD交于点G,使△ABG为等边三角形如图3,求∠AOB的度数.
【答案】
(1)
解:如图1,延长PE,QB交于点F,
∵△APO和△BQO是等腰直角三角形,
∴∠APO=∠BQO=90°,∠AOP=∠BOQ=45°,
∵∠AOB=90°,
∴∠AOP+∠AOB+∠BOQ=180°,
∴点P,O,Q在同一条直线上,
∵∠APO=∠BQO=90°,
∴AP∥BQ,
∴∠PAE=∠FBE,
∵点E是AB中点,
∴AE=BE,
∵∠AEP=∠BEF,
∴△APE≌△BFE,
∴PE=EF,
∴点E是Rt△PQF的斜边PF的中点,
∴EP=EQ;
(2)
解:成立,
证明:∵点C,E分别是OA,AB的中点,
∴CE∥OB,CE= ![]() OB,
OB,
∴∠DOC=∠ECA,
∵点D是Rt△OQB斜边中点,
∴DQ= ![]() OB,
OB,
∴CE=DQ,
同理:PC=DE,∠DOC=∠BDE,
∴∠ECA=∠BDE,
∵∠PCE=∠EDQ,
∴△EPC≌△QED,
∴EP=EQ;
(3)
解:如图2,连接GO,

∵点D,C分别是OB,OA的中点,△APO与△QBO都是等腰直角三角形,
∴CQ,GP分别是OB,OA的垂直平分线,
∴GB=GO=GA,
∴∠GBO=∠GOB,∠GOA=∠GAO,
设∠GOB=x,∠GOA=y,
∴x+x+y+y+60°=360°
∴x+y=150°,
∴∠AOB=150°.
【解析】(1)先判断出点P,O,Q在同一条直线上,再判断出△APE≌△BFE,最后用直角三角形的斜边的中线等于斜边的一半即可得出结论;(2)先判断出CE=DQ,PC=DE,进而判断出△EPC≌△QED即可得出结论;(3)先判断出CQ,GP分别是OB,OA的垂直平分线,进而得出∠GBO=∠GOB,∠GOA=∠GAO,即可得出结论.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
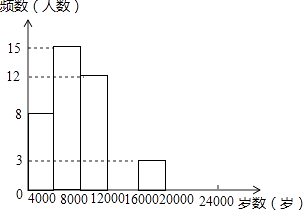
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.