题目内容
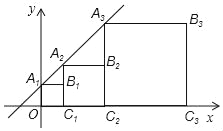
【题目】如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=﹣x2+6x上一点,且在x轴上方,则△BCD面积的最大值为 . 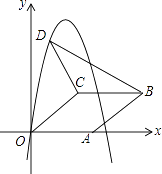
【答案】15
【解析】解:∵D是抛物线y=﹣x2+6x上一点, ∴设D(x,﹣x2+6x),
∵顶点C的坐标为(4,3),
∴OC= ![]() =5,
=5,
∵四边形OABC是菱形,
∴BC=OC=5,BC∥x轴,
∴S△BCD= ![]() ×5×(﹣x2+6x﹣3)=﹣
×5×(﹣x2+6x﹣3)=﹣ ![]() (x﹣3)2+15,
(x﹣3)2+15,
∵﹣ ![]() <0,
<0,
∴S△BCD有最大值,最大值为15,
故答案为15.
设D(x,﹣x2+6x),根据勾股定理求得OC,根据菱形的性质得出BC,然后根据三角形面积公式得出∴S△BCD= ![]() ×5×(﹣x2+6x﹣3)=﹣
×5×(﹣x2+6x﹣3)=﹣ ![]() (x﹣3)2+15,根据二次函数的性质即可求得最大值.
(x﹣3)2+15,根据二次函数的性质即可求得最大值.

练习册系列答案
相关题目