题目内容
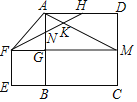
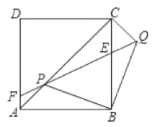
【题目】如图,边长为![]() 的正方形
的正方形![]() 中,P是对角线
中,P是对角线![]() 上的一个动点(点P与A、C不重合),连接
上的一个动点(点P与A、C不重合),连接![]() ,将
,将![]() 绕点B顺时针旋转90°到
绕点B顺时针旋转90°到![]() ,连接
,连接![]() ,
,![]() 与
与![]() 交于点E,
交于点E,![]() 延长线与
延长线与![]() (或
(或![]() 延长线)交于点F.
延长线)交于点F.
(1)连接![]() ,证明:
,证明:![]() ;
;
(2)设![]() ,试写出y关于x的函数关系式,并求当x为何值时,
,试写出y关于x的函数关系式,并求当x为何值时,![]() ;
;
(3)猜想![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
【答案】(1)证明过程见解析;(2)![]() ,当x=3或1时,
,当x=3或1时,![]() ;(3)PF=EQ,证明见解析;
;(3)PF=EQ,证明见解析;
【解析】
(1)证出![]() ,由SAS证明
,由SAS证明![]() 可得结论;
可得结论;
(2)如图证明![]() ,列比利式可得y与x的关系式,根据
,列比利式可得y与x的关系式,根据![]() 计算CE的长,即y的长,代入关系式解方程可得x的值;
计算CE的长,即y的长,代入关系式解方程可得x的值;
(3)如图做辅助线,当F在边AD上时,构建全等三角形,证明![]() ,得EQ=PG,由F、A、G、P四点共圆,得
,得EQ=PG,由F、A、G、P四点共圆,得![]() ,所以△FPG是等腰直角三角形,可得结论;如图,当F在AD延长线上时,同理可得结论.
,所以△FPG是等腰直角三角形,可得结论;如图,当F在AD延长线上时,同理可得结论.
(1)证明:
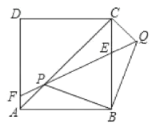
∵线段BP绕点B顺时针旋转![]() 得到线段BQ,
得到线段BQ,
∴BP=BQ,![]() ,
,
∵四边形ABCD是正方形,
∴BA=BC,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
在△BAP和△BCQ中,
∵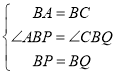 ,
,
∴![]() (SAS),
(SAS),
∴CQ=AP.
(2)如图,

∵四边形ABCD是正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵DC=AD=![]() ,
,
由勾股定理可得:
![]() ,
,
∵AP=x,
∴PC=4-x,
∵△PBQ是等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴ ,
,
由![]() ,
,
∴![]() ,
,
得到![]() ,
,
![]() ,
,
得x=3或x=1.
当x=3或1时,![]() .
.
(3)结论:PF=EQ,理由是:
如图,当F在边AD上时,过P作![]() ,交AB于G,则
,交AB于G,则![]() ,
,
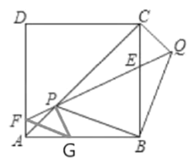
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵PB=BQ,![]() ,
,
∴![]() (SAS),
(SAS),
∴EQ=PG,
∵![]() ,
,
∴F、A、G、P四点共圆,
连接FG,
∴![]() ,
,
∴△FPG是等腰直角三角形,
∴PF=PG,
∴PF=EQ.
当F在AD的延长线上时,如图所示,同理可得:PF=PG=EQ.


练习册系列答案
相关题目