题目内容
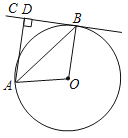
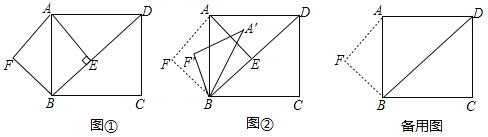
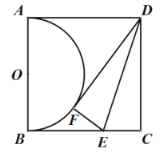
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 是
是![]() 上一点,以
上一点,以![]() 为直径在正方形内作半圆
为直径在正方形内作半圆![]() ,将
,将![]() 沿
沿![]() 翻折,点
翻折,点![]() 刚好落在半圆
刚好落在半圆![]() 上的点
上的点![]() 处,则
处,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
连接DO,OF,根据SSS可以判定△DAO≌△DFO,从而可以得到∠DFO的度数,再根据折叠的性质可知∠DFE=90°,从而可以得到点O、F、E三点共线,然后根据勾股定理,即可求得CE的长,本题得以解决.
连接DO,OF,
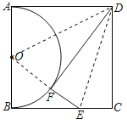
∵四边形ABCD是正方形,将△DCE沿DE翻折得到△DFE,
∴DC=DF,EF=CE,∠DFE=∠C=90°,
∵DC=DA,
∴DA=DF,
在△DAO和△DFO中,
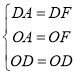 ,
,
∴△DAO≌△DFO(SSS),
∴∠A=∠DFO,
∵∠A=90°,
∴∠DFO=90°,
又∵∠DFE=∠C=90°,
∴∠DFO=∠DFE,
∴点O、F、E三点共线,
设CE=![]() ,则EF=CE=
,则EF=CE=![]() ,OE=OF+EF=
,OE=OF+EF=![]() ,BE=
,BE=![]() ,OB=2,
,OB=2,
∵∠OBE=90°,
∴22+(![]() )2=(
)2=(![]() )2,
)2,
解得,![]() ,
,
即CE的长为![]() ,
,
故选:B.

 名师伴你成长课时同步学练测系列答案
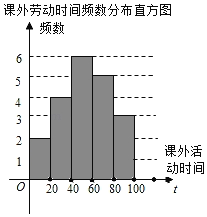
名师伴你成长课时同步学练测系列答案【题目】遵义市各校都在深入开展劳动教育,某校为了解七年级学生一学期参加课外劳动时间(单位:h)的情况,从该校七年级随机抽查了部分学生进行问卷调查,并将调查结果绘制成如下不完整的频数分布表和频数分布直方图.
课外劳动时间频数分布表
劳动时间分组 | 频数 | 频率 |
0≤t<20 | 2 | 0.1 |
20≤t<40 | 4 | m |
40≤t<60 | 6 | 0.3 |
60≤t<80 | a | 0.25 |
80≤t<100 | 3 | 0.15 |
解答下列问题:
(1)频数分布表中a= ,m= ;将频数分布直方图补充完整;
(2)若七年级共有学生400人,试估计该校七年级学生一学期课外劳动时间不少于60h的人数;
(3)已知课外劳动时间在60h≤t<80h的男生人数为2人,其余为女生,现从该组中任选2人代表学校参加“全市中学生劳动体验”演讲比赛,请用树状图或列表法求所选学生为1男1女的概率.