题目内容
【题目】如图，要设计一幅长为3xcm，宽为2ycm的长方形图案，其中有两横两竖的彩条，横彩条的宽度为acm，竖彩条的宽度为bcm，问空白区域的面积是_____．
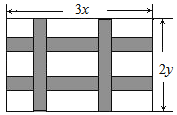
【答案】（6xy﹣6xa﹣4by+4ab）cm2
【解析】
可设想将彩条平移到如图所示的长方形的靠边处，则该长方形的面积就是空白区域的面积，这个大长方形长（3x﹣2b）cm，宽为（2y﹣2a）cm，根据矩形的面积公式求解即可．
解：可设想将彩条平移到如图所示的长方形的靠边处，将9个小矩形组合成“整体”，
一个大的空白长方形，则该长方形的面积就是空白区域的面积．
而这个大长方形长（3x﹣2b）cm，宽为（2y﹣2a）cm．
所以空白区域的面积为（3x﹣2b）（2y﹣2a）cm2．
即（6xy﹣6xa﹣4by+4ab）cm2．
故答案为：（6xy﹣6xa﹣4by+4ab）cm2．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
【题目】在如图中，每个正方形有边长为1 的小正方形组成：
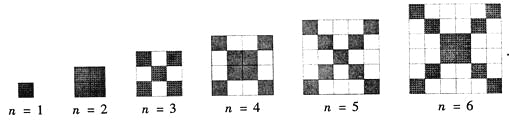
（1） 观察图形，请填写下列表格：
正方形边长 | 1 | 3 | 5 | 7 | … | n(奇数) |
黑色小正方形个数 | … | |||||
正方形边长 | 2 | 4 | 6 | 8 | … | n(偶数) |
黑色小正方形个数 | … |
（2）在边长为n（n≥1）的正方形中，设黑色小正方形的个数为P1，白色小正方形的个数为P2，问是否存在偶数n，使P2＝5P1？若存在，请写出n的值；若不存在，请说明理由.
