题目内容
【题目】已知函数![]() 与x轴、y轴分别交于A、B两点,C点坐标是(0,2),连接AC.
与x轴、y轴分别交于A、B两点,C点坐标是(0,2),连接AC.

(1)直接写出A、B两点的坐标:A(______,_____)、B(_____,_____);
(2)在AB上找一点P,当PC+PO最小时,在AC上找一点Q使得PQ+![]() 最小,求Q点坐标;
最小,求Q点坐标;
(3)在(2)的条件下,平面内能否找到一点K,使得点A、C、P、K构成的四边形是平行四边形,若能,直接写出K点坐标,若不能,请说明理由.
【答案】(1)(![]() ,0),(0,6);(2)Q(
,0),(0,6);(2)Q(![]() );(3)能,K(
);(3)能,K(![]() ,
,![]() )或K(
)或K(![]() ,
,![]() )或K(
)或K(![]() ,
,![]() ).
).
【解析】
(1)在一次函数解析式中,分别令y=0和x=0即可求出A、B的坐标;
(2)作点O关于AB的对称点O′,连接C O′与AB交于P点,则P点即为使得CP+OP最小的点.过O′作O′D⊥x轴.可求出 O′的坐标,O′C的解析式.由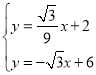 得P的坐标.过Q作QH⊥x轴于H,与AC交于Q点.由含30°直角三角形的性质可得QH=
得P的坐标.过Q作QH⊥x轴于H,与AC交于Q点.由含30°直角三角形的性质可得QH=![]() AQ,即可得到当PH⊥x轴时与AC交点Q即为所求,即可得出点Q的坐标;
AQ,即可得到当PH⊥x轴时与AC交点Q即为所求,即可得出点Q的坐标;
(3)设K(x,y),点A、C、P、K构成的四边形是平行四边形,分三种情况讨论:
①若AK,CP是对角线;②若AP,CK是对角线;③若AC,KP是对角线,;分别利用平行四边形对角线的交点平分对角线和中点坐标公式即可得出点K的坐标.
(1)在![]() 中,令y=0,解得:x=
中,令y=0,解得:x=![]() ,令x=0,解得:y=6,∴A(
,令x=0,解得:y=6,∴A(![]() ,0),B(0,6);
,0),B(0,6);
(2)作点O关于AB的对称点O′,连接C O′与AB交于P点,则P点即为使得CP+OP最小的点.过O′作O′D⊥x轴.
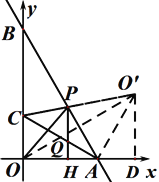
∵OA=![]() ,OB=6,∴AB=
,OB=6,∴AB=![]() ,∴∠ABO=30,∠BAO=60,∴O′A=OA=
,∴∠ABO=30,∠BAO=60,∴O′A=OA=![]() ,∠O′AB=∠OAB=60 ∴∠O'AD=60°,∴∠AO'D=30°,∴O′D=3,AD=
,∠O′AB=∠OAB=60 ∴∠O'AD=60°,∴∠AO'D=30°,∴O′D=3,AD=![]() ,∴ O′(
,∴ O′(![]() ,3),易求O′C解析式为:
,3),易求O′C解析式为:![]() .
.
由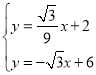 得P(
得P(![]() ,
,![]() ).
).
过Q作QH⊥x轴于H,与AC交于Q点.
∵OC=2,OA=![]() ,∴∠CAO=30,∴QH=
,∴∠CAO=30,∴QH=![]() AQ,∴当PH⊥x轴时与AC交点Q即为所求.
AQ,∴当PH⊥x轴时与AC交点Q即为所求.
易求直线AC的解析式为![]() ,把x=
,把x=![]() 代入
代入![]() ,得y=
,得y=![]() ,∴Q(
,∴Q(![]() ).
).
(3)设K(x,y).
∵P(![]() ,
,![]() ),A(
),A(![]() ,0),C(0,2),点A、C、P、K构成的四边形是平行四边形,∴分三种情况讨论:
,0),C(0,2),点A、C、P、K构成的四边形是平行四边形,∴分三种情况讨论:
①若AK,CP是对角线,则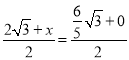 ,
,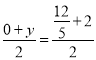 ,解得:x=
,解得:x=![]() ,y=
,y=![]() ,∴ K(
,∴ K(![]() ,
,![]() );
);
②若AP,CK是对角线,则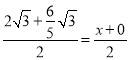 ,
,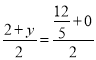 ,解得:x=
,解得:x=![]() ,y=
,y=![]() ,∴ K(
,∴ K(![]() ,
,![]() );
);
③若AC,KP是对角线,则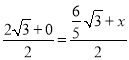 ,
,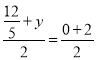 ,解得:x=
,解得:x=![]() ,y=
,y=![]() ,∴ K(
,∴ K(![]() ,
,![]() );
);
综上所述:K(![]() ,
,![]() )或K(
)或K(![]() ,
,![]() )或K(
)或K(![]() ,
,![]() ).
).

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案