Question

【题目】如图，已知平行四边形OACB的顶点O、A、B的坐标分别是（0，0）、（0，a），（b，0），且a、b满足

（1）如图1，求点C的坐标；

（2）如图2，点P为边OB上一动点，作等腰Rt△APD，且∠APD=90°．当点P从O运动到点B的过程中，求点D运动路程的长度；

（3）如图3，在（2）的条件下，作等腰Rt△BED，且∠DBE=90°，再作等腰Rt△ECF，且∠ECF=90°，直线FE分别交AC、OB于点M、N，求证：FM=EN．

Answer 1

【答案】（1）C（4，4）；（2）；（3）证明见解析

【解析】

（1）根据+(2a-8)2=0可知2a-8=0，解得a=4，a=b，则b=4，A(0，4)，B(4，0)，可知OA=OB，四边形OACB为平行四边形，∠AOB=90°，则四边形OACB为正方形，可得C(4，4)．

（2）点P的运动轨迹为一条线段，则点D的运动轨迹也为一条线段，当点P与点O重合时，点D与点B重合，当点P与点B重合时，点D的位置如图1所示，点D的运动路径为BD，算出BD=4．

（3）由（2）点D的运动路径可知点D在∠OBC的外角平分线上，过点F作FG垂直AC于点G，过E作EH垂直AC于点H，已知△FCE为等腰直角三角形，可推出△FGC≌△CHE（AAS），过点E作EQ垂直OB于点Q，可推出△FGM≌△ENQ（AAS），可得FM=EN．

解：（1）∵+(2a-8)2=0

∴2a-8=0，解得a=4，

∵a=b，

∴b=4，

∴A(0，4)，B(4，0)，

∴OA=OB，

∵四边形OACB为平行四边形，∠AOB=90°，

∴四边形OACB为正方形，

∴C(4，4)．

（2）如图1所示，

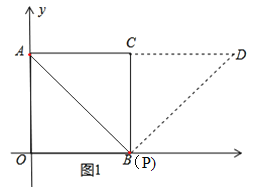
∵点P的运动轨迹为一条线段，则点D的运动轨迹也为一条线段，

当点P与点O重合时，点D与点B重合，当点P与点B重合时，因为△APD是等腰直角三角形，所以A、C、D三点共线，点D的位置如图1所示，此时△BCD是等腰直角三角形，

∴点D的运动路径为BD，

∴BD=4．

（3）如图2所示，

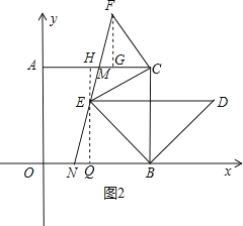
由（2）点D的运动路径可知点D在∠OBC的外角平分线上，

∴∠DBC=∠EBC=∠EBO=45°，

∴ED//OB，

过点F作FG垂直AC于点G，过E作EH垂直AC于点H，

∴∠FGC=∠EHC=90°，

∵△FCE为等腰直角三角形，

∴FC=EC，∠FCE=90°，

∵∠ACB=90°，

∴∠FCG=∠ECB=∠CEH，

∴△FGC≌△CHE（AAS），

∴CH=FG，

过点E作EQ垂直OB于点Q，

则BQ=EQ=CH=FG，

∵∠FGM=∠EQN=90°，∠FMG=∠ENQ，

∴△FGM≌△ENQ（AAS），

∴FM=EN．