题目内容
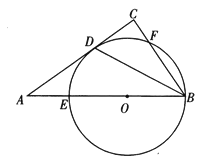
【题目】如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,与AC交于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.
(1)求证:AC是⊙O的切线;
(2)已知AB=10,BC=6,求⊙O的半径r.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接OD.欲证AC是⊙O的切线,只需证明AC⊥OD即可;
(2)利用平行线截线段成比例推知![]() ;然后将图中线段间的和差关系代入该比例式,通过解方程即可求得r的值,即⊙O的半径r的值.
;然后将图中线段间的和差关系代入该比例式,通过解方程即可求得r的值,即⊙O的半径r的值.
试题解析:(1)证明:连接OD.
∵OB=OD,
∴∠OBD=∠ODB(等角对等边);
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ODB=∠DBC(等量代换),
∴OD∥BC(内错角相等,两直线平行);
又∵∠C=90°(已知),
∴∠ADO=90°(两直线平行,同位角相等),
∴AC⊥OD,即AC是⊙O的切线;
(2)解:由(1)知,OD∥BC,
∴![]() (平行线截线段成比例),
(平行线截线段成比例),
∴![]() ,
,
解得r=![]() ,即⊙O的半径r为
,即⊙O的半径r为![]() .
.


练习册系列答案
相关题目
