题目内容
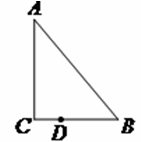
如图,P是正方形ABCD内一点,∠APB=1350 ,BP=1,AP=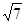
,求PC的值（ ）
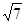,求PC的值（ ）A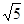． | B．3 | C．2 | D．2 |
B.
试题分析：解答此题的关键是利用旋转构建直角三角形，由勾股定理求解.如图，把△PBC绕点B逆时针旋转90°得到△ABP′，点C的对应点C′与点A重合.根据旋转的性质可得AP′=PC，BP′=BP，△PBP′是等腰直角三角形，利用勾股定理求出
，然后由∠APB=1350 ,可得出∠APP′=90°，再利用勾股定理列式计算求出
.故选B.
练习册系列答案
优质课堂快乐成长系列答案
相关题目
后,得到的图案是（ ）
