题目内容
如图,抛物线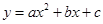 与
与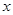 轴交于
轴交于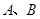 两点,与
两点,与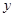 轴相交于点
轴相交于点 .连结AC、BC,B、C两点的坐标分别为B(1,0)、
.连结AC、BC,B、C两点的坐标分别为B(1,0)、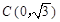 ,且当x=-10和x=8时函数的值
,且当x=-10和x=8时函数的值 相等.
相等.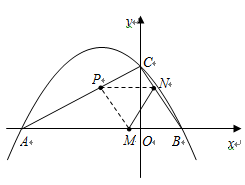
【小题1】求a、b、c的值;
【小题2】若点
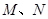 同时从
同时从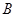 点出发,均以每秒1个单位长度的速度分别沿
点出发,均以每秒1个单位长度的速度分别沿 边运动,其中一个点到达终点时,另一点也随之停止运动.连结
边运动,其中一个点到达终点时,另一点也随之停止运动.连结 ,将
,将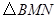 沿
沿 翻折,当运动时间为几秒时,
翻折,当运动时间为几秒时,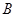 点恰好落在
点恰好落在 边上的
边上的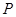 处?并求点
处?并求点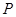 的坐标及四边形
的坐标及四边形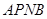 的面积;
的面积;【小题3】上下平移该抛物线得到新的抛物线,设新抛物线的顶点为D,对称轴与x轴的交点为E,若△ODE与△OBC相似,求新抛物线的解析式。
【小题1】
∵当x=-10和x=8时函数的值
 相等
相等∴抛物线的对称轴为直线x=-1,
由题意得:a+b+c=0,c=
 ,
,

∴

【小题2】令y=0,则 x=-3或1,∴A(-3,0)易得

∴△ABC为直角三角形,∠ACB=90°,∠A=30°,∠B=60°
∴BM=BN=PN=PM,∴四边形BNPM为菱形.
设运动t秒后点B在AC上,
∵PN∥AB,∴

过P作PE⊥AB于E,在RT△PBN中,


,四边形
 的面积=
的面积=
【小题3】
① 当
 时
时 ;
;② 当
 时
时 ;
; ③ 当
 时
时
④ 当
 时
时 解析:
解析:p;【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 轴交于
轴交于 (2)点
(2)点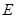 为抛物线上一动点,在
为抛物线上一动点,在 ,使以
,使以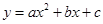 与
与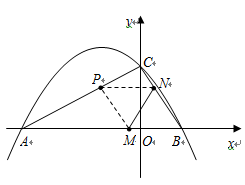
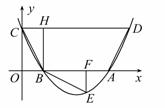
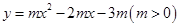 与
与 轴交于
轴交于 两点,与
两点,与 轴交于
轴交于 点.
点.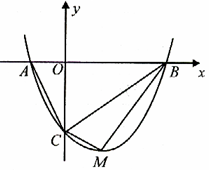
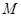 的坐标(用含
的坐标(用含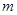 的代数式表示),
的代数式表示), 与
与 的面积比不变,试求出这个比值;
的面积比不变,试求出这个比值;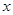 轴交于
轴交于 (
( ,0)、
,0)、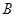 (
( ,0)两点,且
,0)两点,且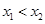 ,与
,与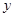 轴交于点
轴交于点 ,其中
,其中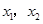 是方程
是方程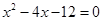 的两个根。(14分)
的两个根。(14分) (2)点
(2)点 是线段
是线段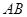 上的一个动点,过点
上的一个动点,过点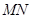 ∥
∥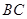 ,交
,交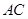 于点
于点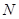 ,连接
,连接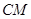 ,当
,当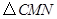 的面积最大时,求点
的面积最大时,求点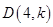 在(1)中抛物线上,
在(1)中抛物线上,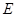 为抛物线上一动点,在
为抛物线上一动点,在 ,使以
,使以 为顶
为顶