题目内容
我们知道，对于实系数方程ax2+bx+c=0（a≠0），若x1、x2是其两实数根，则有ax2+bx+c=a（x-x1）（x-x2）=ax2-a（x1+x2）x+ax1x2，故有b=-a（x1+x2），c=ax1x2，即得x1+x2=-
，x1x2=
．
根据上述内容，若实系数方程ax3+bx2+cx+d=0（a≠0）的三个实数根分别是x1、x2、x3，则x1+x2+x3=______； x1x2x3=______．
| b |
| a |
| c |
| a |
根据上述内容，若实系数方程ax3+bx2+cx+d=0（a≠0）的三个实数根分别是x1、x2、x3，则x1+x2+x3=______； x1x2x3=______．
根据题意可得
ax3+bx2+cx+d
=a（x-x1）（x-x2）（x-x3）
=a（x2-xx1-xx2+x1x2）（x-x3）
=a（x3-x2x1-x2x2+xx1x2-x2x3+xx1x3+xx2x3-x1x2x3）
=ax3-a（x1+x2+x3）x2+a（x1x2+x1x3+x2x3）x-ax1x2x3，
∴b=-a（x1+x2+x3），d=-ax1x2x3，
即得x1+x2+x3=-
，x1x2x3=-
．
故答案为：-
，-
．
ax3+bx2+cx+d
=a（x-x1）（x-x2）（x-x3）
=a（x2-xx1-xx2+x1x2）（x-x3）
=a（x3-x2x1-x2x2+xx1x2-x2x3+xx1x3+xx2x3-x1x2x3）
=ax3-a（x1+x2+x3）x2+a（x1x2+x1x3+x2x3）x-ax1x2x3，
∴b=-a（x1+x2+x3），d=-ax1x2x3，
即得x1+x2+x3=-
| b |
| a |
| d |
| a |
故答案为：-
| b |
| a |
| d |
| a |
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
，x1x2=
．
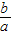，x1x2=
．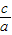