题目内容
【题目】已知:如图,△ABC中,AB=AC,D、E分别在AC、AB上,且BD=BC,AD=DE=EB, 则∠A的度数等于( )
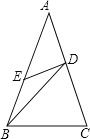
A. 36°B. 40°C. 45°D. 50°
【答案】C
【解析】
根据同一个三角形中等边对等角的性质,设∠ABD=x,结合三角形外角的性质,则可用x的代数式表示∠A、∠ABC、∠C,再在△ABC中,运用三角形的内角和为180°,可求∠A的度数.
∵DE=EB,
∴设∠BDE=∠ABD=x,
∴∠AED=∠BDE+∠ABD=2x,
∵AD=DE,
∴∠A=∠AED=2x,
∴∠BDC=∠A+∠ABD=3x,
∵BD=BC,
∴∠C=∠BDC=3x,
∵AB=AC,
∴∠ABC=∠C=3x,
在△ABC中,3x+3x+2x=180°,
解得x=22.5°,
∴∠A=2x=22.5°×2=45°,
故选C.

练习册系列答案
相关题目
【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?