题目内容
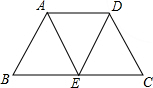 在等腰梯形ABCD中,AD∥BC,E是BC的中点,连接AE,DE,AE与DE相等吗?
在等腰梯形ABCD中,AD∥BC,E是BC的中点,连接AE,DE,AE与DE相等吗?(1)请说明理由.
(2)上题中,若添加条件BC=2AD,图中有平行四边形吗?请指出来,并说明理由.
分析:(1)利用等腰梯形的性质得出AB=DC,∠B=∠C结合E是BC的中点可证明△ABE≌△DCE,利用全等三角形的性质即可证得两对应线段相等.
(2)由题意可得出AD∥BC,AD=BE=EC,从而根据平行四边形的判定得出四边形ADEB及四边形ADCE是平行四边形.
(2)由题意可得出AD∥BC,AD=BE=EC,从而根据平行四边形的判定得出四边形ADEB及四边形ADCE是平行四边形.
解答:解:AE和DE相等.
(1)理由:∵四边形ABCD是等腰梯形,
∴AB=DC,∠B=∠C.
∵E是BC的中点,
∴BE=CE.
在△ABE和△DCE中,
,
∴△ABE≌△DCE(SAS).
∴AE=DE.
(2)由题意得:AD∥BC,且AB=BE=EC,
∴可判断四边形ADEB及四边形ADCE是平行四边形.
(1)理由:∵四边形ABCD是等腰梯形,
∴AB=DC,∠B=∠C.
∵E是BC的中点,
∴BE=CE.
在△ABE和△DCE中,
|
∴△ABE≌△DCE(SAS).
∴AE=DE.
(2)由题意得:AD∥BC,且AB=BE=EC,
∴可判断四边形ADEB及四边形ADCE是平行四边形.
点评:本题考查等腰梯形的性质、平行四边形的判定及全等三角形的判定及性质,有一定的综合性,难度不大,掌握平行四边形的判定定理及等腰梯形的性质是关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且 24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.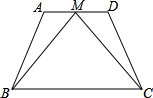 如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么?
如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么? 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.