题目内容
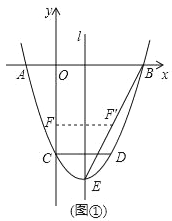
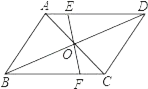
【题目】如图,△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交线段DE的延长线相交于F点,取AF的中点G,如果BC=2AB.
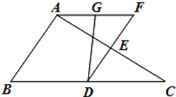
求证 :(1)四边形ABDF是菱形;
(2)AC=2DG.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)首先根据三角形的中位线定理,得DE∥AB,结合AF∥BC,根据两组对边分别平行的四边形是平行四边形,可以判断该四边形是平行四边形,再根据一组邻边相等的平行四边形是菱形即可证明;
(2)根据菱形的性质可以进一步得到△FGD≌△FEA,则GD=AE,即可证明结论.
证明:(1)∵点D、E分别是边BC、AC的中点,
∴DE是△ABC的中位线(三角形中位线的定义),
∴DE∥AB,DE=![]() AB(三角形中位线性质).
AB(三角形中位线性质).
∵AF∥BC,
∴四边形ABDF是平行四边形(平行四边形定义).
∵BC=2AB,BC=2BD,
∴AB=BD.
∴四边形ABDF是菱形.
(2)∵四边形ABDF是菱形,
∴AF=AB=DF(菱形的四条边都相等).
∵DE=![]() AB,
AB,
∴EF=![]() AF.
AF.
∵G是AF的中点.
∴GF=![]() AF,
AF,
∴GF=EF.
∴△FGD≌△FEA,
∴GD=AE,
∵AC=2EC=2AE,
∴AC=2DG.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目