题目内容
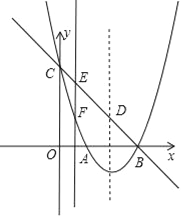
【题目】如图，在平面直角坐标系中，O为坐标原点，点A在反比例函数y=
（x > 0)的图象上，作AB⊥y轴于B点.
(1) △ABO的面积为 .
(2) 若点A的横坐标为4，点P在x轴的正半轴.且△OAP是等腰三角形，求点P的坐标: .
(3)动点M从原点出发，沿x轴的正方向运动，以MA为直角边，在MA的右侧作等腰Rt△MAN=90°,若在点M运动过程中，斜边MN始终在x轴上，求ON-OM的值
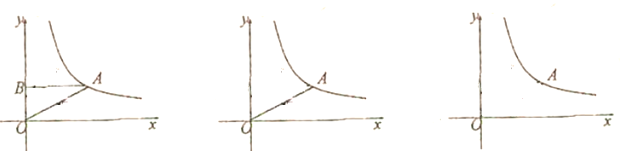
【答案】（1）6；（2）（5,0）或（8,0）或（
,0）；（3）48.
【解析】
（1）根据反比例函数系数k的几何意义，即可求出△ABO的面积；
（2）先求出点A的坐标，设点P的坐标为（a，0）由题意可知：a＞0，根据平面直角坐标系中任意两点之间的距离公式，即可求出OA=
，OP=a，AP=
，然后根据等腰三角形的腰的情况分类讨论即可；
（3）过点A作AB⊥x轴于B，设点A的坐标为（x，y），则OB·AB=x·y=12，根据等腰直角三角形的性质，可得：AB=MB=BN，然后根据平方差公式，即可求出ON-OM的值.
解：（1）∵点A在反比例函数y=
（x > 0)的图象上，AB⊥y轴
∴S△ABO=
故答案为：6；
（2）将x=4代入y=中，得：y=3
∴点A的坐标为（4,3）
设点P的坐标为（a，0）由题意可知：a＞0
∴OA=，OP=a，AP=
①当OA=OP时，如下图所示
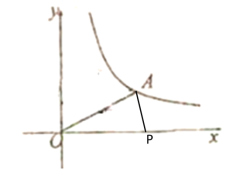
∴a=5
此时点P的坐标为（5,0）；
②当OA=AP时，如下图所示
∴
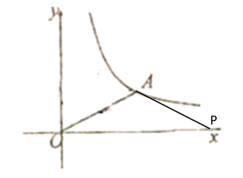
解得：
（不符合a的取值范围，舍去），
此时点P的坐标为（8,0）；
③当OP=AP时，如下图所示
∴
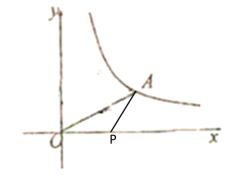
解得：
此时点P的坐标为（,0）.
综上所述：点P的坐标为（5,0）或（8,0）或（,0）；
（3）如图所示，过点A作AB⊥x轴于B
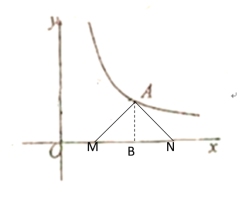
∴OB·AB=x·y=12
∵△AMN为等腰直角三角形，AB⊥x轴
∴AB=MB=BN
∴ON-OM
=（ON-OM）（ON+OM）
=MN（OB+BN+OB-BM）
=（MB+BN）（OB+BN+OB-BM）
=（AB + AB）（OB+ AB +OB- AB）
=2AB·2OB
=4AB·OB
=48
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
