题目内容
【题目】如图,等边△ABC中,AM为边BC上的中线,动点D在直线AM上,以CD为一边在CD的下方作等边△CDE,设直线BE与直线AM的交点为O.
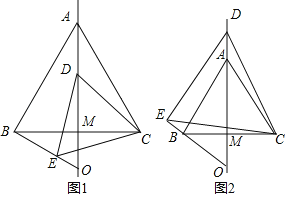
(1)如图1,点D在线段AM上时,填空:
①线段AD与BE的数量关系是 ②∠AOB的度数是 .
(2)如图2,当动点D在线段MA的延长线上时,试判断(1)中的结论是否成立?若成立,请给予证明:若不成立,请写出新的结论,并说明理由.
【答案】(1)①AD=BE;②60°;(2)成立,理由见解析
【解析】
(1)①证明△ACD≌△BCE即可.
②先证明∠CAM=30°,由△ACD≌△BCE得∠OBM=∠CAM=30°,由此即可解决问题.
(2)结论不变.证明方法类似(1).
(1)∵△ABC和△DCE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
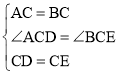 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE;
故答案为:AD=BE;
②∵BM=CM,AB=AC,∠BAC=60°,
∴AM⊥BC,∠BAM=∠CAM=30°,
∴∠AMC=∠MBO=90°,
∵△ACD≌△BCE,
∴∠OBM=∠CAM=30°,
∵∠OBM+∠BOM=90°
∴∠AOB=60°;
故答案为:60°;
(2)(1)中的结论成立,理由如下:
∵△ABC和△DCE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=∠BCE,
∵BM=CM,AB=AC,∠BAC=60°,
∴AM⊥BC,∠BAM=∠CAM=30°,
∴∠AMC=∠MBO=90°,
在△ACD和△BCE中,
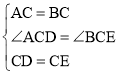 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠DAC=∠EBC,
∴∠OBM=∠CAM=30°,
∴∠AOB=90°﹣∠OBM=60°.

【题目】甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | |
学生甲 | 90 | 94 | 86 | 90 |
学生乙 | 94 | 82 | 93 | 91 |
(1)分别计算甲、乙成绩的平均数和方差;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?