题目内容
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.

【答案】(1)证明参见解析;(2)2![]() -
-![]() .
.
【解析】
试题分析:(1)连接半径CO,证明OC⊥CD即可得出结论;(2)图中阴影部分面积用直角三角形COD的面积减去扇形COB的面积即可.
试题解析:(1)连接OC.
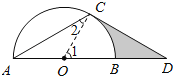 ,∵AC=CD,∠ACD=120°,∴∠A=∠D=30°.∵OA=OC,
,∵AC=CD,∠ACD=120°,∴∠A=∠D=30°.∵OA=OC,
∴∠2=∠A=30°.∴∠OCD=180°﹣∠A﹣∠D﹣∠2=180-30-30-30=90°.即OC⊥CD,OC又是半径,∴CD是⊙O的切线.(2)由图可知∠1=2∠2=60,又因为OC=2,所以在直角三角形COD中,CD=2![]() ,图中阴影部分面积用直角三角形COD的面积减去扇形COB的面积,即=2×2
,图中阴影部分面积用直角三角形COD的面积减去扇形COB的面积,即=2×2![]() ÷2-
÷2- =2
=2![]() -
-![]() .所以图中阴影部分的面积是2
.所以图中阴影部分的面积是2![]() -
-![]() .
.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
