题目内容
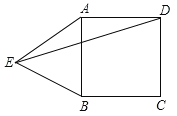
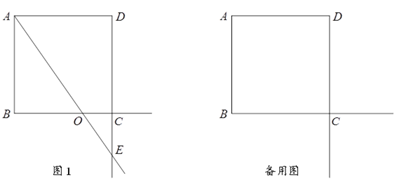
【题目】如图,正方形ABCD的边长为36cm,点O以6cm/s的速度从点B沿射线BC方向运动,射线AO交直线DC于点E.设点O运动的时间为t s.
⑴ 当t=9时,DE的长为 cm;
⑵ 设DE=y,求y关于t的函数关系式;
⑶ 在线段BO上取点G,使得OC∶OG=4∶5.当以OC为半径的⊙O与直线AG相切时,求t的值.
【答案】(1)DE=24cm;(2) ![]() (t>0);(3) t的值为
(t>0);(3) t的值为![]() 或12.
或12.
【解析】分析:(1)根据题意画出图形,再利用相似三角形的判定与性质得出答案;(2)利用相似三角形的判定与性质得出y关于t的函数关系式;(3)分别利用当点O在BC边上,及当点O在BC延长线上时,得出点t的值.
详解:⑴DE=24cm.
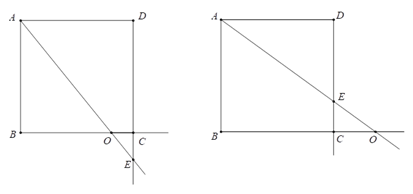
图1 图2
⑵由正方形ABCD得:∠B=∠D=90°,AB∥DC
由题意得:BO=6t
∵ AB∥CD ∴ ∠BAO=∠AED
∴ △ABO∽△EDA
∴ ![]()
∴ ![]() ,整理得:
,整理得:![]()
∴ y关于x的函数关系式为:![]() (t>0).
(t>0).
⑶设OC=4x,则OG=5x
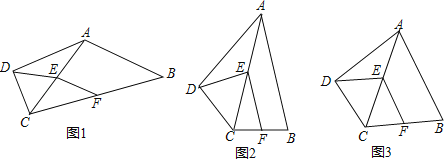
ⅰ如图3,当点O在BC边上,⊙O切AG于点P,OP=OC=4x
△OGP中,∠OPG=90°,
∴ ![]()
∴ tan∠OGP=![]()
∴ tan∠AGB=![]()
△ABG中,∠B=90° tan∠AGB=![]() ,解得:BG=27
,解得:BG=27
∴ BC=27+5x+4x=36 解得:x=1
∴ ![]() s
s
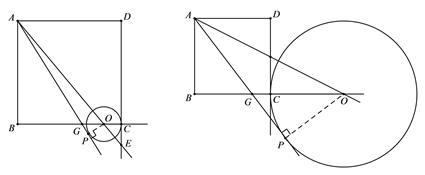
图3 图4
ⅱ如图3,当点O在BC的延长线上时,⊙O切AG于点P,OP=OC=4x
同ⅰ可得:BG=27
∴ BC=27+5x-4x=36 解得:x=9
∴ ![]() s
s
综上:当以OC为半径的⊙O与直线AG相切时,t的值为![]() 或12.
或12.
点睛:本题考查了圆的综合,勾股定理的应用及相似三角形的判定与性质等知识,正确分类讨论是解答本题的关键.

练习册系列答案
相关题目