题目内容
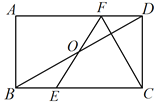
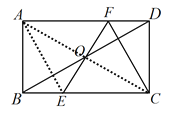
【题目】如图,点O为矩形ABCD对角线BD的中点,直线EF经过点O分别与边BC,AD交于点E, F,连接CF,若∠CEF=2∠CBD,∠CBD =30°,DC=![]() ,有下面的结论:①FD=BE;②∠EOD=150°;③BE2+AB2=AF2;④BC=6;⑤直线FC是线段OD的垂直平分线.其中正确的个数为( )个.
,有下面的结论:①FD=BE;②∠EOD=150°;③BE2+AB2=AF2;④BC=6;⑤直线FC是线段OD的垂直平分线.其中正确的个数为( )个.
A. 2B. 3C. 4D. 5
【答案】D
【解析】
根据矩形的性质易证△BOE≌△DOF,可得FD=BE,所以①正确;由∠CEF=∠CBO +∠BOE=2∠CBD,求出∠CBO =∠BOE=30°,可得∠EOD=150°,所以②正确;根据一组对边平行且相等的四边形是平行四边形证明四边形AECF是平行四边形,根据矩形的性质结合∠CBD =30°证明△OCD为等边三角形,求出∠EOC=90°可得平行四边形AECF是菱形,得到AE=AF,由勾股定理可得BE2+AB2=AF2,所以③正确;根据含30°直角三角形的性质可求出BC=6,故④正确;根据等角对等边得到FO=FD,根据等边三角形的性质得到CO=CD,可得直线FC是线段OD的垂直平分线,所以⑤正确.
解:∵AD∥BC,
∴∠FDO =∠EBO,
又∵∠FOD =∠EOB,OB=OD,
∴△BOE≌△DOF(ASA),
∴FD=BE,故①正确;
∵∠CEF=∠CBO +∠BOE=2∠CBD,
∴∠CBO =∠BOE=30°,
∴∠EOD=180°-30°=150°,故②正确;
连结AE,AC,
∵FD=BE,
∴AF=EC,
∵AD∥BC,
∴四边形AECF是平行四边形,
∵∠CBD =30°,
∴∠BDC=60°,
∵OC=OD,
∴△OCD为等边三角形,
∴∠OCD=60°,
∴∠OCE=30°,
∵∠CEF=2∠CBD=60°,
∴∠EOC=90°,即AC⊥EF,
∴平行四边形AECF是菱形,
∴AE=AF,
∵BE2+AB2=AE2,
∴BE2+AB2=AF2,故③正确;
∵∠CBD =30°,DC=![]() ,∠BCD=90°,
,∠BCD=90°,
∴BC=![]() DC=6,故④正确;
DC=6,故④正确;
∵△BOE≌△DOF,
∴∠CBO =∠BOE=∠FDO =∠FOD,
∴FO=FD,
∵△OCD为等边三角形,
∴CO=CD,
∴直线FC是线段OD的垂直平分线,故⑤正确,
正确的有5个,
故选:D.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
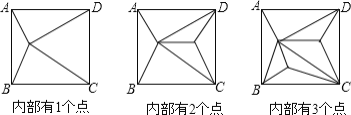
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 |
|
| … |
|
(2)原正方形能否被分割成2019个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.