题目内容
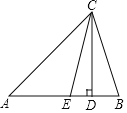
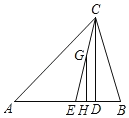
【题目】如图,在△ABC中,CD是AB边上的高,CE是∠ACB的平分线.
(1)若∠A=40°,∠B=76°,求∠DCE的度数;
(2)若∠A=α,∠B=β,求∠DCE的度数(用含α,β的式子表示);
(3)当线段CD沿DA方向平移时,平移后的线段与线段CE交于G点,与AB交于H点,若∠A=α,∠B=β,求∠HGE与α、β的数量关系.
【答案】(1)∠DCE=18°;(2)∠DCE![]() β
β![]() α;(3)∠HGE
α;(3)∠HGE![]() β
β![]() α.
α.
【解析】
(1)根据三角形的内角和得到∠ACB的度数,根据角平分线的定义得到∠ECB的度数,根据余角的定义得到∠BCD=90°-∠B,于是得到结论;
(2)根据角平分线的定义得到∠ACB=180°-α-β,根据角平分线的定义得到∠ECB=![]() ∠ACB=
∠ACB=![]() (180°-α-β),根据余角的定义得到∠BCD=90°-∠B=90°-β,于是得到结论;
(180°-α-β),根据余角的定义得到∠BCD=90°-∠B=90°-β,于是得到结论;
(3)运用(2)中的方法,得到∠DCE=∠ECB-∠BCD=![]() β-
β-![]() α,再根据平行线的性质,即可得出结论.
α,再根据平行线的性质,即可得出结论.
(1)∵∠A=40°,∠B=76°,
∴∠ACB=64°.
∵CE是∠ACB的平分线,
∴∠ECB![]() ∠ACB=32°.
∠ACB=32°.
∵CD是AB边上的高,
∴∠BDC=90°,
∴∠BCD=90°﹣∠B=14°,
∴∠DCE=∠ECB﹣∠BCD=32°﹣14°=18°;
(2)∵∠A=α,∠B=β,
∴∠ACB=180°﹣α﹣β.
∵CE是∠ACB的平分线,
∴∠ECB![]() ∠ACB
∠ACB![]() (180°﹣α﹣β).
(180°﹣α﹣β).
∵CD是AB边上的高,
∴∠BDC=90°,
∴∠BCD=90°﹣∠B=90°﹣β,
∴∠DCE=∠ECB﹣∠BCD![]() β
β![]() α;
α;
(3)如图所示.
∵∠A=α,∠B=β,
∴∠ACB=180°﹣α﹣β.
∵CE是∠ACB的平分线,
∴∠ECB![]() ∠ACB
∠ACB![]() (180°﹣α﹣β).
(180°﹣α﹣β).
∵CD是AB边上的高,
∴∠BDC=90°,
∴∠BCD=90°﹣∠B=90°﹣β,
∴∠DCE=∠ECB﹣∠BCD![]() β
β![]() α,
α,
由平移可得:GH∥CD,
∴∠HGE=∠DCE![]() β
β![]() α.
α.

 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案