题目内容
 14、如图所示,在等腰梯形ABCD中,AB∥CD,∠A=60°,AB=9,CD=5,BC的长是( )
14、如图所示,在等腰梯形ABCD中,AB∥CD,∠A=60°,AB=9,CD=5,BC的长是( )分析:∵等腰梯形ABCD,过D、C分别作梯形的高DE、CF,∴DC=EF AE=FB∴FB=AE=$frac{1}{2}$(AB-CD)=2,又∵∠A=60°,∴BC=AD=4.
解答: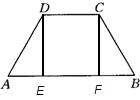 解:过D、C分别作梯形的高DE、CF,垂足分别为E、F
解:过D、C分别作梯形的高DE、CF,垂足分别为E、F
∵在等腰梯形ABCD中,AB∥CD,AB=9,CD=5,DE,CF分别为高
∴EF=CD=5,AE=BF=2
∵∠A=60°
∴AD=BC=4
故选B.
 解:过D、C分别作梯形的高DE、CF,垂足分别为E、F
解:过D、C分别作梯形的高DE、CF,垂足分别为E、F∵在等腰梯形ABCD中,AB∥CD,AB=9,CD=5,DE,CF分别为高
∴EF=CD=5,AE=BF=2
∵∠A=60°
∴AD=BC=4
故选B.
点评:主要考查学生对等腰梯形的性质等知识点的掌握情况,做题时要对已知进行灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且 1、如图所示,在等腰梯形ABCD中,AD∥BC,DE⊥BC于点E,BF⊥AE于点F,请你添加一个条件,使△ABF≌△CDE.
1、如图所示,在等腰梯形ABCD中,AD∥BC,DE⊥BC于点E,BF⊥AE于点F,请你添加一个条件,使△ABF≌△CDE. 48、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,DE⊥BC于E,BF⊥AE于F,AE=BE.请你判断线段BF与图形中哪条线段相等,先写出你的猜想,再加以证明.
48、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,DE⊥BC于E,BF⊥AE于F,AE=BE.请你判断线段BF与图形中哪条线段相等,先写出你的猜想,再加以证明.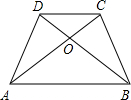 如图所示,在等腰梯形ABCD中,AB∥CD,若AB+CD=4,并且∠AOB=120°,则该等腰梯形的面积为
如图所示,在等腰梯形ABCD中,AB∥CD,若AB+CD=4,并且∠AOB=120°,则该等腰梯形的面积为 如图所示,在等腰梯形ABCD中,AD∥BC,过A作腰CD的平行线,AE∥CD,AB=AD=DC,∠B=60°
如图所示,在等腰梯形ABCD中,AD∥BC,过A作腰CD的平行线,AE∥CD,AB=AD=DC,∠B=60°