Question

如图，在□ABCD中，AB＝5，AD＝10，cosB＝，过BC的中点E作EF⊥AB，垂足为点F，连结DF，求DF的长．

Answer 1

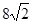
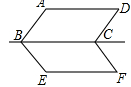
试题分析：首先延长DC，FE相交于点H，由四边形ABCD是平行四边形，E是BC的中点，易得△BFE≌△CHE，又由cosB=，EF⊥AB，在Rt△BFE中，由三角函数的定义，可求得BF的长，由勾股定理，可求得EF、DH的长，然后在Rt△FHD中，由勾股定理，求得DF的长．
延长DC，FE相交于点H

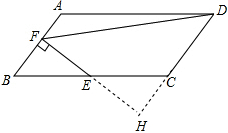
∵四边形ABCD是平行四边形，
∴AB∥DC，AB=CD，AD=BC，
∴∠B=∠ECH，∠BFE=∠H．
∵AB=5，AD=10，
∴BC=10，CD=5．
∵E是BC的中点，
∴BE=EC=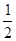BC=5．
∴△BFE≌△CHE（AAS），
∴CH=BF，EF=EH．
∵EF⊥AB，
∴∠BFE=∠H=90°．
在Rt△BFE中，
∵cosB=
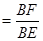∴BF=CH=3．
∴，DH=8．
在Rt△FHD中，∠H=90°，
∴
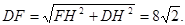
点评：此题难度适中，注意掌握辅助线的作法是解此题的关键，同时注意数形结合思想的应用．