Question

【题目】如图，AC是ABCD的对角线，在AD边上取一点F，连接BF交AC于点E，并延长BF交CD的延长线于点G．

（1）若∠ABF＝∠ACF，求证：CE2＝EFEG；

（2）若DG＝DC，BE＝6，求EF的长．

Answer 1

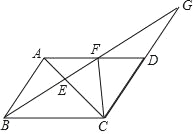
【答案】（1）证明见解析；（2）3.

【解析】

（1）依据等量代换得到∠ECF=∠G，依据∠CEF=∠CEG，可得△ECF∽△EGC，进而得出，即CE2=EFEG；
（2）依据AB=CD=DG，可得AB：CG=1：2，依据AB∥CG，即可得出EG=12，BG=18，再根据AB∥DG，可得，进而得到EF=BF-BE=9-6=3．

解：（1）∵AB∥CG，

∴∠ABF＝∠G，

又∵∠ABF＝∠ACF，

∴∠ECF＝∠G，

又∵∠CEF＝∠CEG，

∴△ECF∽△EGC，

∴，即CE2＝EFEG；

（2）∵平行四边形ABCD中，AB＝CD，

又∵DG＝DC，

∴AB＝CD＝DG，

∴AB：CG＝1：2，

∵AB∥CG，

∴，

即，

∴EG＝12，BG＝18，

∵AB∥DG，

∴，

∴BF＝BG＝9，

∴EF＝BF﹣BE＝9﹣6＝3．